I changed the finite element space to 2,however, even when the density is 1kg/m^3, it does not converge. Additionally, the boundary condition at the wall,is set as 0, but the results show the velocity at the wall has several points not equal to 0, what may be the reason for this? ![]()

The mf.xdmf file show the wall region is 3, like this:

Two questions:
- please drop
bcp_out, and try again. Does it converge, or not? - please report the Reynolds number for the case of density equal to 1, and Re for the case of viscosity & density equal to the one of the blood.
- This is the new script, I changed to IPCS method to solve the ns equations:
Additionally, dropbcp_outmeans reducing the outlet pressure boundary conditions? I changed it to 166Pa, and it doesn’t converge either.
import meshio
import matplotlib.pyplot as plt
from dolfin import *
#msh = meshio.read("import_stl.msh")
mesh = Mesh()
with XDMFFile("pipe_cad.xdmf") as infile:
infile.read(mesh)
##
mvc = MeshValueCollection("size_t", mesh, 2)
with XDMFFile("mf_pipe_cad.xdmf") as infile:
infile.read(mvc, "name_to_read")
mf = cpp.mesh.MeshFunctionSizet(mesh, mvc)
boundary_markers=MeshFunction("size_t",mesh,mvc)
##
mvc = MeshValueCollection("size_t", mesh, 3)
with XDMFFile("cf_pipe_cad.xdmf") as infile:
infile.read(mvc, "name_to_read")
cf = cpp.mesh.MeshFunctionSizet(mesh, mvc)
T=1
in_marker=1
out_marker=2
wall_marker=3
domain_marker=4
#deltat=T/num_steps
dt=0.005
num_steps=200
mu=0.0035
rho=1.060
nu=mu/rho
V=VectorFunctionSpace(mesh,"CG",2) #velocity space
Q=FunctionSpace(mesh,"P",1) #pressure space
bcu_in=DirichletBC(V,Constant((0.037386,-0.002018,0.196464)),boundary_markers,in_marker)
#bcp_in=DirichletBC(Q,Constant(2000),boundary_markers,in_marker)
bcp_out=DirichletBC(Q,Constant(166.61),boundary_markers,out_marker)
bcu_wall=DirichletBC(V,Constant((0.0,0.0,0.0)),boundary_markers,wall_marker)
bcu=[bcu_in,bcu_wall]
bcp=[bcp_out]
# t=n (u,p) unknown
#u_ = Function(V)
#p_ = Function(Q)
# t=n-1 known
#u_1 = Function(V)
#p_1 = Function(Q)
# Create functions
# Define coefficients
k = Constant(dt)
#f = Constant((0, 0, 0))
# Define trial and test functions
u = TrialFunction(V)
v = TestFunction(V)
p = TrialFunction(Q)
q = TestFunction(Q)
# Define functions for solutions at previous and current time steps
u_n = Function(V)
u_ = Function(V)
p_n = Function(Q)
p_ = Function(Q)
# Define expressions used in variational forms
U = 0.5*(u_n + u)
n = FacetNormal(mesh)
f = Constant((0.0, 0.0, 0.0))
k = Constant(dt)
mu = Constant(mu)
rho = Constant(rho)
# Define symmetric gradient
def epsilon(u):
return sym(nabla_grad(u))
# Define stress tensor
def sigma(u,p):
return 2*mu*epsilon(u)-p*Identity(len(u))
# Define variational problem for step 1
F1 = rho*dot((u-u_n)/k,v)*dx\
+ rho*dot(dot(u_n,nabla_grad(u_n)),v)*dx\
+ inner(sigma(U,p_n),epsilon(v))*dx\
+ dot(p_n*n,v)*ds-dot(mu*nabla_grad(U)*n,v)*ds\
- dot(f,v)*dx
a1 = lhs(F1)
L1 = rhs(F1)
# Define variational problem for step 2
a2 = dot(nabla_grad(p),nabla_grad(q))*dx
L2 = dot(nabla_grad(p_n),nabla_grad(q))*dx-(1/k)*div(u_)*q*dx
# Define variational problem for step 3
a3 = dot(u,v)*dx
L3 = dot(u_,v)*dx-k*dot(nabla_grad(p_-p_n),v)*dx
# Assemble matrices
# Apply boundary conditions to matrices
# Use amg preconditioner if available
#prec = "amg" if has_krylov_solver_preconditioner("amg") else "default"
# Use nonzero guesses - essential for CG with non-symmetric BC
#parameters['krylov_solver']['nonzero_initial_guess'] = True
# Create files for storing solution
ufile = File("mpi_v2_p166/velocity_cad_rho1060.pvd")
pfile = File("mpi_v2_p166/pressure_cad_rho1060.pvd")
# Time-stepping
t = 0
#while t < T + DOLFIN_EPS:
for n in range(num_steps):
A1 = assemble(a1)
A2 = assemble(a2)
A3 = assemble(a3)
[bc.apply(A1) for bc in bcu]
[bc.apply(A2) for bc in bcp]
t=t+dt
print(t)
# Update pressure boundary condition
#p_in.t = t
begin("Computing tentative velocity")
# Compute tentative velocity step
b1 = assemble(L1)
[bc.apply(b1) for bc in bcu]
solve(A1, u_.vector(), b1, "cg", "sor")
end()
begin("Computing pressure correction")
# Pressure correction
b2 = assemble(L2)
[bc.apply(b2) for bc in bcp]
#[bc.apply(p1.vector()) for bc in bcp]
solve(A2, p_.vector(), b2, "cg", "sor")
end()
begin("Computing velocity correction")
# Velocity correction
b3 = assemble(L3)
#[bc.apply(A3, b3) for bc in bcu]
solve(A3, u_.vector(), b3, "cg", "sor")
end()
# Save to file
ufile << u_
pfile << p_
print("max u_", u_.vector().max())
print("min u_", u_.vector().min())
print("max p_", p_.vector().max())
print("min p_", p_.vector().min())
# Move to next time step
u_n.assign(u_)
p_n.assign(p_)
# Plot solution
#plt.figure()
#plot(p1, title="Pressure")
#plt.figure()
#plot(u1, title="Velocity")
#plt.show()
The error:
0.4550000000000003
Computing tentative velocity
Computing pressure correction
Computing velocity correction
max u_ 2.3821763731909925e+139
min u_ -3.1133783161542936e+139
max p_ 2.6536879350175624e+137
min p_ -2.4941021179589655e+138
0.4600000000000003
Computing tentative velocity
Traceback (most recent call last):
File "tipe_ns_IPCS.py", line 133, in <module>
solve(A1, u_.vector(), b1, "cg", "sor")
File "/public/home/cxr1/.conda/envs/fenicss/lib/python3.8/site-packages/dolfin/fem/solving.py", line 227, in solve
return dolfin.la.solver.solve(*args)
File "/public/home/cxr1/.conda/envs/fenicss/lib/python3.8/site-packages/dolfin/la/solver.py", line 72, in solve
return cpp.la.solve(A, x, b, method, preconditioner)
RuntimeError:
*** -------------------------------------------------------------------------
*** DOLFIN encountered an error. If you are not able to resolve this issue
*** using the information listed below, you can ask for help at
***
*** fenics-support@googlegroups.com
***
*** Remember to include the error message listed below and, if possible,
*** include a *minimal* running example to reproduce the error.
***
*** -------------------------------------------------------------------------
*** Error: Unable to solve linear system using PETSc Krylov solver.
*** Reason: Solution failed to converge in 0 iterations (PETSc reason DIVERGED_NANORINF, residual norm ||r|| = inf).
*** Where: This error was encountered inside PETScKrylovSolver.cpp.
*** Process: 0
***
*** DOLFIN version: 2019.1.0
*** Git changeset: 2e001bd1aae8e14d758264f77382245e6eed04b0
*** -------------------------------------------------------------------------
The pressure distribution is like this:
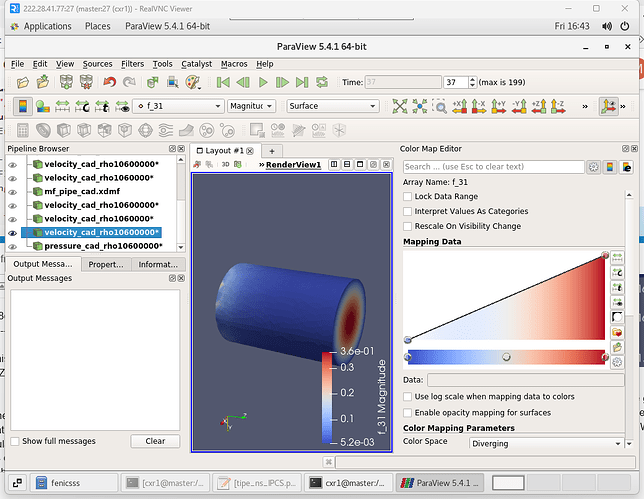
And the velocity magnitude is: (Wall still has some points bigger than zero)
- The viscosity is 0.0035 Pa·s, the character length L (the diameter of pipe geometry) is 0.011 m, the velocity magnitude at the inlet is 0.2 m/s. When the density equal to 1kg/m^3, according to the calculation formula of Reynolds number,Re is 0.6286. When density is 1060kg/m^3(blood density), Re is equal to 666.2857.

Hi! Really sorry to bother you. Do you have any new suggestions on this issue?
Please drop altogether setting the pressure at the outlet. I understand the rationale (enforcing a physiological pressure), but FE for Navier-Stokes equation typically doesn’t have Dirichlet conditions for pressure (especially not at outlets), and thus I’d like to understand if that is the cause of non-convergence.
Furthermore, if you are using iterative solvers for the linear system, please drop them as well and use sparse direct solvers, e.g. mumps. You can re-enable them later, but first I’d like you to test on the simpler case in which you use the direct solver.
I set the pressure at the outlet as 0Pa, and it still doesn’t converge. ![]() Additionally, the pressure inlet and velocity outlet doesn’t converge either.
Additionally, the pressure inlet and velocity outlet doesn’t converge either.
Setting it to 0 and dropping that BC are not the same thing.
Hi! Do you mean I should exclude the pressure boundary condition? I changed the script to this and it still not converge ![]()
![]() :
:
import meshio
import matplotlib.pyplot as plt
from dolfin import *
#msh = meshio.read("import_stl.msh")
mesh = Mesh()
with XDMFFile("pipe_cad.xdmf") as infile:
infile.read(mesh)
##
mvc = MeshValueCollection("size_t", mesh, 2)
with XDMFFile("mf_pipe_cad.xdmf") as infile:
infile.read(mvc, "name_to_read")
mf = cpp.mesh.MeshFunctionSizet(mesh, mvc)
boundary_markers=MeshFunction("size_t",mesh,mvc)
##
mvc = MeshValueCollection("size_t", mesh, 3)
with XDMFFile("cf_pipe_cad.xdmf") as infile:
infile.read(mvc, "name_to_read")
cf = cpp.mesh.MeshFunctionSizet(mesh, mvc)
T=1
in_marker=1
out_marker=2
wall_marker=3
domain_marker=4
#deltat=T/num_steps
dt=0.005
num_steps=200
mu=0.0035
rho=1060
nu=mu/rho
V=VectorFunctionSpace(mesh,"P",2) #velocity space
Q=FunctionSpace(mesh,"P",1) #pressure space
bcu_in=DirichletBC(V,Constant((0.037386,-0.002018,0.196464)),boundary_markers,in_marker)
#bcp_in=DirichletBC(Q,Constant(2000),boundary_markers,in_marker)
#bcp_out=DirichletBC(Q,Constant(0),boundary_markers,out_marker)
bcu_out=DirichletBC(V,Constant((0.047386,-0.003018,0.206464)),boundary_markers,out_marker)
bcu_wall=DirichletBC(V,Constant((0.0,0.0,0.0)),boundary_markers,wall_marker)
bcu=[bcu_in,bcu_out,bcu_wall]
#bcp=[bcp_out]
ds=Measure("ds",domain=mesh,subdomain_data=mf)
dx=Measure("dx",domain=mesh,subdomain_data=cf)
# t=n (u,p) unknown
#u_ = Function(V)
#p_ = Function(Q)
# t=n-1 known
#u_1 = Function(V)
#p_1 = Function(Q)
# Create functions
# Define coefficients
k = Constant(dt)
#f = Constant((0, 0, 0))
# Define trial and test functions
u = TrialFunction(V)
v = TestFunction(V)
p = TrialFunction(Q)
q = TestFunction(Q)
# Define functions for solutions at previous and current time steps
u_n = Function(V)
u_ = Function(V)
p_n = Function(Q)
p_ = Function(Q)
# Define expressions used in variational forms
U = 0.5*(u_n + u)
n = FacetNormal(mesh)
f = Constant((0.0, 0.0, 0.0))
k = Constant(dt)
mu = Constant(mu)
rho = Constant(rho)
# Define symmetric gradient
def epsilon(u):
return sym(nabla_grad(u))
# Define stress tensor
def sigma(u,p):
return 2.0*mu*epsilon(u)-p*Identity(len(u))
# Define variational problem for step 1
F1 = rho*dot((u-u_n)/k,v)*dx\
+ rho*dot(dot(u_n,nabla_grad(u_n)),v)*dx\
+ inner(sigma(U,p_n),epsilon(v))*dx\
+ dot(p_n*n,v)*ds-dot(mu*nabla_grad(U)*n,v)*ds\
- dot(f,v)*dx
#F1=(1/k)*inner(v,u-u_n)*dx+inner(v,grad(u_n)*u_n)*dx+inner(epsilon(v),sigma(U,p_n))*dx-nu*inner(grad(U)*n, v)*ds+inner(v, p_n*n)*ds-inner(v,f)*dx
a1 = lhs(F1)
L1 = rhs(F1)
# Define variational problem for step 2
a2 = dot(nabla_grad(p),nabla_grad(q))*dx
L2 = dot(nabla_grad(p_n),nabla_grad(q))*dx-(1/k)*div(u_)*q*dx
# Define variational problem for step 3
a3 = dot(u,v)*dx
L3 = dot(u_,v)*dx-k*dot(nabla_grad(p_-p_n),v)*dx
# Assemble matrices
# Apply boundary conditions to matrices
# Use amg preconditioner if available
#prec = "amg" if has_krylov_solver_preconditioner("amg") else "default"
# Use nonzero guesses - essential for CG with non-symmetric BC
#parameters['krylov_solver']['nonzero_initial_guess'] = True
# Create files for storing solution
ufile = File("mpi_v2_nop/velocity_cad_rho1060.pvd")
pfile = File("mpi_v2_nop/pressure_cad_rho1060.pvd")
# Time-stepping
t = 0
#while t < T + DOLFIN_EPS:
for n in range(num_steps):
A1 = assemble(a1)
A2 = assemble(a2)
A3 = assemble(a3)
[bc.apply(A1) for bc in bcu]
#[bc.apply(A2) for bc in bcp]
t=t+dt
print(t)
# Update pressure boundary condition
#p_in.t = t
begin("Computing tentative velocity")
# Compute tentative velocity step
b1 = assemble(L1)
[bc.apply(b1) for bc in bcu]
solve(A1, u_.vector(), b1, "gmres", "default")
end()
begin("Computing pressure correction")
# Pressure correction
b2 = assemble(L2)
#[bc.apply(b2) for bc in bcp]
#[bc.apply(p1.vector()) for bc in bcp]
solve(A2, p_.vector(), b2, "gmres", "amg")
end()
begin("Computing velocity correction")
# Velocity correction
b3 = assemble(L3)
#[bc.apply(A3, b3) for bc in bcu]
solve(A3, u_.vector(), b3, "bicgstab", "default")
end()
# Save to file
ufile << u_
pfile << p_
print("max u_", u_.vector().max())
print("min u_", u_.vector().min())
print("max p_", p_.vector().max())
print("min p_", p_.vector().min())
# Move to next time step
u_n.assign(u_)
p_n.assign(p_)
# Plot solution
#plt.figure()
#plot(p1, title="Pressure")
#plt.figure()
#plot(u1, title="Velocity")
#plt.show()
The error message:
0.005
Computing tentative velocity
Calling FFC just-in-time (JIT) compiler, this may take some time.
Computing pressure correction
Computing velocity correction
max u_ 0.7380555475783942
min u_ -0.32688779528508316
max p_ 36978080285440.04
min p_ 36978080285438.54
0.01
Computing tentative velocity
Computing pressure correction
Computing velocity correction
max u_ 1.7467538436517016
min u_ -1.2093201956874324
max p_ 22323540412097.95
min p_ 22323540412096.816
0.015
Computing tentative velocity
Computing pressure correction
Computing velocity correction
max u_ 5.099527460549027
min u_ -4.659722125919449
max p_ 11514606807001.104
min p_ 11514606807000.348
0.02
Computing tentative velocity
Computing pressure correction
Computing velocity correction
max u_ 59.18461015940818
min u_ -93.32504700463994
max p_ 25712224969191.96
min p_ 25712224969185.387
0.025
Computing tentative velocity
Computing pressure correction
Computing velocity correction
max u_ 5691.286295265366
min u_ -6022.039298651888
max p_ 17273629475645.541
min p_ 17273629475385.162
0.030000000000000002
Computing tentative velocity
Computing pressure correction
Computing velocity correction
max u_ 138978391.23414996
min u_ -68944350.05794688
max p_ -17084010179995.195
min p_ -17084011973509.863
0.035
Computing tentative velocity
Computing pressure correction
Computing velocity correction
max u_ 1.3503353138059274e+16
min u_ -2.248557073197942e+16
max p_ 1143093675346757.0
min p_ 719876489283017.5
0.04
Computing tentative velocity
Computing pressure correction
Computing velocity correction
max u_ 5.909914710418386e+32
min u_ -9.329035999658654e+32
max p_ 1.8026508252866507e+31
min p_ -2.8445978449030676e+30
0.045
Computing tentative velocity
Computing pressure correction
Computing velocity correction
max u_ 1.5843123255490923e+66
min u_ -3.325445579480316e+66
max p_ -8.354509624999246e+65
min p_ -8.69820471700155e+65
0.049999999999999996
Computing tentative velocity
Computing pressure correction
Computing velocity correction
max u_ 6.262610790977613e+132
min u_ -9.536354137353314e+132
max p_ 1.7348792898284515e+131
min p_ 2.8797955596101976e+129
0.05499999999999999
Computing tentative velocity
Traceback (most recent call last):
File "tipe_ns_IPCS.py", line 135, in <module>
solve(A1, u_.vector(), b1, "gmres", "default")
File "/public/home/cxr1/.conda/envs/fenicss/lib/python3.8/site-packages/dolfin/fem/solving.py", line 227, in solve
return dolfin.la.solver.solve(*args)
File "/public/home/cxr1/.conda/envs/fenicss/lib/python3.8/site-packages/dolfin/la/solver.py", line 72, in solve
return cpp.la.solve(A, x, b, method, preconditioner)
RuntimeError:
*** -------------------------------------------------------------------------
*** DOLFIN encountered an error. If you are not able to resolve this issue
*** using the information listed below, you can ask for help at
***
*** fenics-support@googlegroups.com
***
*** Remember to include the error message listed below and, if possible,
*** include a *minimal* running example to reproduce the error.
***
*** -------------------------------------------------------------------------
*** Error: Unable to solve linear system using PETSc Krylov solver.
*** Reason: Solution failed to converge in 0 iterations (PETSc reason DIVERGED_NANORINF, residual norm ||r|| = inf).
*** Where: This error was encountered inside PETScKrylovSolver.cpp.
*** Process: 0
***
*** DOLFIN version: 2019.1.0
*** Git changeset: 2e001bd1aae8e14d758264f77382245e6eed04b0
*** --------------------------------------------------------------------
The mesh points I convinced the unit is meter, like this:
$MeshFormat
4.1 0 8
$EndMeshFormat
$PhysicalNames
4
2 1 "in"
2 2 "out"
2 3 "wall"
3 4 "domain"
$EndPhysicalNames
$Entities
4 6 4 1
1 -0.0266614914008932 -0.0343508721144389 -0.891873605983566 0
2 -0.0233827375262053 -0.0345278333385147 -0.874643688463323 0
3 -0.0151560930206336 -0.0343508721144389 -0.8940630169006401 0
4 -0.0118773391459457 -0.0345278333385147 -0.876833099380397 0
1 -0.0266615914008932 -0.03452793333851468 -0.891873705983566 -0.0233826375262054 -0.0343507721144389 -0.874643588463323 0 2 1 -2
2 -0.02666160200293606 -0.04020660508641883 -0.8940646543762392 -0.0151559930206336 -0.0343507721144389 -0.8918735059835661 0 2 3 -1
3 -0.0151561930206336 -0.03452793333851468 -0.89406311690064 -0.0118772391459458 -0.0343507721144389 -0.876832999380397 0 2 4 -3
4 -0.02338284812824817 -0.04038356631049464 -0.8768347368559962 -0.01187723914594569 -0.0345277333385147 -0.8746435884633231 0 2 4 -2
5 -0.02338283752620532 -0.03452793333851471 -0.8768331993803969 -0.01187722854390283 -0.02867210036653477 -0.8746420509877239 0 2 2 -4
6 -0.0266615914008932 -0.0343509721144389 -0.8940631169006399 -0.01515598241859074 -0.02849513914245897 -0.8918719685079668 0 2 1 -3
1 -0.02666160200293609 -0.0403835663104946 -0.8940646543762393 -0.01187723914594577 -0.03435077211443887 -0.8746435884633228 1 3 4 -1 -2 -3 4
2 -0.02666159140089323 -0.03452793333851468 -0.89406311690064 -0.01187722854390292 -0.02849513914245897 -0.8746420509877235 1 3 4 1 5 3 -6
Yes, exactly, without that BC.
Can you try replacing all solve(.., ..., ..., "...", "...") with solve(.., ..., ..., "lu", "mumps"), to see if the issue is the iterative solver?
As you said, I changed the solver, but it can’t solve from the first step.
import meshio
import matplotlib.pyplot as plt
from dolfin import *
#msh = meshio.read("import_stl.msh")
mesh = Mesh()
with XDMFFile("pipe_cad.xdmf") as infile:
infile.read(mesh)
##
mvc = MeshValueCollection("size_t", mesh, 2)
with XDMFFile("mf_pipe_cad.xdmf") as infile:
infile.read(mvc, "name_to_read")
mf = cpp.mesh.MeshFunctionSizet(mesh, mvc)
boundary_markers=MeshFunction("size_t",mesh,mvc)
##
mvc = MeshValueCollection("size_t", mesh, 3)
with XDMFFile("cf_pipe_cad.xdmf") as infile:
infile.read(mvc, "name_to_read")
cf = cpp.mesh.MeshFunctionSizet(mesh, mvc)
T=1
in_marker=1
out_marker=2
wall_marker=3
domain_marker=4
#deltat=T/num_steps
dt=0.005
num_steps=200
mu=0.0035
rho=1060
nu=mu/rho
V=VectorFunctionSpace(mesh,"P",2) #velocity space
Q=FunctionSpace(mesh,"P",1) #pressure space
bcu_in=DirichletBC(V,Constant((0.037386,-0.0021189,0.2062872)),boundary_markers,in_marker)
#u=0.03 Re=100
#bcu_in=DirichletBC(V,Constant((0.0056079,-0.0003027,0.0294696)),boundary_markers,in_marker)
#bcp_in=DirichletBC(Q,Constant(1),boundary_markers,in_marker)
#bcp_out=DirichletBC(Q,Constant(666),boundary_markers,out_marker)
bcu_out=DirichletBC(V,Constant((0.0392553,-0.003018,0.206464)),boundary_markers,out_marker)
bcu_wall=DirichletBC(V,Constant((0.0,0.0,0.0)),boundary_markers,wall_marker)
bcu=[bcu_in,bcu_out,bcu_wall]
#bcu=[bcu_wall]
#bcu=[bcu_in,bcu_wall]
#bcp=[bcp_out]
#bcp=[bcp_in,bcp_out]
#bcp=[bcp_out]
ds=Measure("ds",domain=mesh,subdomain_data=mf)
dx=Measure("dx",domain=mesh,subdomain_data=cf)
# t=n (u,p) unknown
#u_ = Function(V)
#p_ = Function(Q)
# t=n-1 known
#u_1 = Function(V)
#p_1 = Function(Q)
# Create functions
# Define coefficients
k = Constant(dt)
#f = Constant((0, 0, 0))
# Define trial and test functions
u = TrialFunction(V)
v = TestFunction(V)
p = TrialFunction(Q)
q = TestFunction(Q)
# Define functions for solutions at previous and current time steps
u_n = Function(V)
u_ = Function(V)
p_n = Function(Q)
p_ = Function(Q)
# Define expressions used in variational forms
U = 0.5*(u_n + u)
n = FacetNormal(mesh)
f = Constant((0.0, 0.0, 0.0))
k = Constant(dt)
mu = Constant(mu)
rho = Constant(rho)
# Define symmetric gradient
def epsilon(u):
return sym(nabla_grad(u))
# Define stress tensor
def sigma(u,p):
return 2.0*mu*epsilon(u)-p*Identity(len(u))
# Define variational problem for step 1
F1 = rho*dot((u-u_n)/k,v)*dx\
+ rho*dot(dot(u_n,nabla_grad(u_n)),v)*dx\
+ inner(sigma(U,p_n),epsilon(v))*dx\
+ dot(p_n*n,v)*ds-dot(mu*nabla_grad(U)*n,v)*ds\
- dot(f,v)*dx
#F1=(1/k)*inner(v,u-u_n)*dx+inner(v,grad(u_n)*u_n)*dx+inner(epsilon(v),sigma(U,p_n))*dx-nu*inner(grad(U)*n, v)*ds+inner(v, p_n*n)*ds-inner(v,f)*dx
a1 = lhs(F1)
L1 = rhs(F1)
# Define variational problem for step 2
a2 = dot(nabla_grad(p),nabla_grad(q))*dx
L2 = dot(nabla_grad(p_n),nabla_grad(q))*dx-(1/k)*div(u_)*q*dx
# Define variational problem for step 3
a3 = dot(u,v)*dx
L3 = dot(u_,v)*dx-k*dot(nabla_grad(p_-p_n),v)*dx
# Assemble matrices
# Apply boundary conditions to matrices
# Use amg preconditioner if available
#prec = "amg" if has_krylov_solver_preconditioner("amg") else "default"
# Use nonzero guesses - essential for CG with non-symmetric BC
#parameters['krylov_solver']['nonzero_initial_guess'] = True
# Create files for storing solution
ufile = File("ipcs_rho1060_u_v2/velocity_cad_rho1060.pvd")
pfile = File("ipcs_rho1060_u_v2/pressure_cad_rho1060.pvd")
# Time-stepping
t = 0
#while t < T + DOLFIN_EPS:
for n in range(num_steps):
A1 = assemble(a1)
A2 = assemble(a2)
A3 = assemble(a3)
[bc.apply(A1) for bc in bcu]
#[bc.apply(A2) for bc in bcp]
t=t+dt
print(t)
# Update pressure boundary condition
#p_in.t = t
begin("Computing tentative velocity")
# Compute tentative velocity step
b1 = assemble(L1)
[bc.apply(b1) for bc in bcu]
solve(A1, u_.vector(), b1, "lu", "mumps")
end()
begin("Computing pressure correction")
# Pressure correction
b2 = assemble(L2)
#[bc.apply(b2) for bc in bcp]
#[bc.apply(p1.vector()) for bc in bcp]
solve(A2, p_.vector(), b2, "lu", "mumps")
end()
begin("Computing velocity correction")
# Velocity correction
b3 = assemble(L3)
#[bc.apply(A3, b3) for bc in bcu]
solve(A3, u_.vector(), b3, "lu", "mumps")
end()
# Save to file
ufile << u_
pfile << p_
print("max u_", u_.vector().max())
print("min u_", u_.vector().min())
print("max p_", p_.vector().max())
print("min p_", p_.vector().min())
# Move to next time step
u_n.assign(u_)
p_n.assign(p_)
The error message:
$ python tipe_ns_IPCS.py
0.005
Computing tentative velocity
Traceback (most recent call last):
File "tipe_ns_IPCS.py", line 141, in <module>
solve(A1, u_.vector(), b1, "lu", "mumps")
File "/public/home/cxr1/.conda/envs/fenicss/lib/python3.8/site-packages/dolfin/fem/solving.py", line 227, in solve
return dolfin.la.solver.solve(*args)
File "/public/home/cxr1/.conda/envs/fenicss/lib/python3.8/site-packages/dolfin/la/solver.py", line 72, in solve
return cpp.la.solve(A, x, b, method, preconditioner)
RuntimeError:
*** -------------------------------------------------------------------------
*** DOLFIN encountered an error. If you are not able to resolve this issue
*** using the information listed below, you can ask for help at
***
*** fenics-support@googlegroups.com
***
*** Remember to include the error message listed below and, if possible,
*** include a *minimal* running example to reproduce the error.
***
*** -------------------------------------------------------------------------
*** Error: Unable to solve linear system.
*** Reason: Preconditioner may not be specified for LU solver.
*** Where: This error was encountered inside LinearSolver.cpp.
*** Process: 0
***
*** DOLFIN version: 2019.1.0
*** Git changeset: 2e001bd1aae8e14d758264f77382245e6eed04b0
*** ----------------------------------------------------------
OK, have a look in the documentation of solve what is the right combination of the input argument to use mumps
I find mumps is a solver for this:
Solver method | Description
------------------------------------------------------------------------------
bicgstab | Biconjugate gradient stabilized method
cg | Conjugate gradient method
default | default linear solver
gmres | Generalized minimal residual method
minres | Minimal residual method
mumps | MUMPS (MUltifrontal Massively Parallel Sparse direct Solver)
petsc | PETSc built in LU solver
richardson | Richardson method
superlu | SuperLU
superlu_dist | Parallel SuperLU
tfqmr | Transpose-free quasi-minimal residual method
umfpack | UMFPACK (Unsymmetric MultiFrontal sparse LU factorization)
So I changed the code to this:
begin("Computing tentative velocity")
# Compute tentative velocity step
b1 = assemble(L1)
[bc.apply(b1) for bc in bcu]
solve(A1, u_.vector(), b1, "mumps", "default")
end()
begin("Computing pressure correction")
# Pressure correction
b2 = assemble(L2)
#[bc.apply(b2) for bc in bcp]
#[bc.apply(p1.vector()) for bc in bcp]
solve(A2, p_.vector(), b2, "mumps", "default")
end()
begin("Computing velocity correction")
# Velocity correction
b3 = assemble(L3)
#[bc.apply(b3) for bc in bcu]
solve(A3, u_.vector(), b3, "mumps", "default")
end()
And the velocity and pressure become Nan for this:
0.3200000000000002
Computing tentative velocity
Computing pressure correction
Computing velocity correction
max u_ nan
min u_ nan
max p_ nan
min p_ nan
When rho=1,it seems to be converge, but the pressure is too large:
0.09500000000000001
Computing tentative velocity
Computing pressure correction
Computing velocity correction
max u_ 0.4955111248797407
min u_ -0.11295611069414253
max p_ 1395760840678.9053
min p_ 1395760840675.6387