How to get the first order derivative of the solution and store it in a numpy array

[dokken]

@kalosu

Could it be possible to project or interpolate the DG-0 derivative results into a Lagrange-1 function?

Doing so introduces Gibb’s phenomenon, as explained in: Projection and interpolation — FEniCS Tutorial @ Sorbonne

What you could do is to take the average from all cells associated with a given vertex, as it would not introduce oscillations as Gibb’s.

To do so I would loop through each vertex and find the connecting cells for each vertex and extract the values, i.e.

from mpi4py import MPI
import numpy as np
import dolfinx

mesh = dolfinx.mesh.create_unit_square(MPI.COMM_WORLD, 20, 20)


V = dolfinx.fem.functionspace(mesh, ("Lagrange", 1))
Q = dolfinx.fem.functionspace(mesh, ("DG", 0))

q = dolfinx.fem.Function(Q)
q.name = "DG0"
# Mark some of the cells with 3, the others with 7
left_cells = dolfinx.mesh.locate_entities(mesh, mesh.topology.dim, lambda x: (x[0] <= 0.5+1e-14) & (x[1] <= 0.3+1e-14))
q.x.array[:] = 7
q.interpolate(lambda x: np.full(x.shape[1], 3.0), cells=left_cells)
q.x.scatter_forward()

num_vertices = mesh.topology.index_map(
    0).size_local + mesh.topology.index_map(0).num_ghosts
mesh.topology.create_connectivity(0, mesh.topology.dim)
v_to_c = mesh.topology.connectivity(0, mesh.topology.dim)
geom_nodes = dolfinx.mesh.entities_to_geometry(mesh, 0, np.arange(num_vertices,dtype=np.int32), False)

dof_layout = V.dofmap.dof_layout
vertex_to_dof_map = np.empty(num_vertices, dtype=np.int32)
num_cells = mesh.topology.index_map(
    mesh.topology.dim).size_local + mesh.topology.index_map(
    mesh.topology.dim).num_ghosts
c_to_v = mesh.topology.connectivity(mesh.topology.dim, 0)
for cell in range(num_cells):
    vertices = c_to_v.links(cell)
    dofs = V.dofmap.cell_dofs(cell)
    for i, vertex in enumerate(vertices):
        vertex_to_dof_map[vertex] = dofs[dof_layout.entity_dofs(0, i)]

u = dolfinx.fem.Function(V)
for i, node in enumerate(geom_nodes):
    cells = v_to_c.links(i)
    value = 0
    for cell in cells:
        value+=q.x.array[cell]
    value/=len(cells)
    u.x.array[vertex_to_dof_map[i]] = value
u.name = "P1"
u.x.scatter_forward()
with dolfinx.io.XDMFFile(mesh.comm, "output.xdmf", "w") as xdmf:
    xdmf.write_mesh(mesh)
    xdmf.write_function(u)
    xdmf.write_function(q)

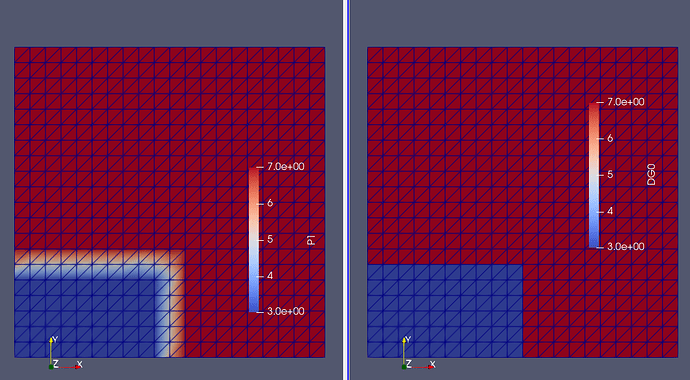
yielding

[kalosu]

Hello there @dokken,

I am now trying to solve a PDE system in where the gradient of a known function is involved. At the moment I include the gradient term in my UFL expression as inner(grad(f),grad(v)*dx.

I wonder if this is the correct way to include the gradient of my known scalar function in this case. My scalar function is defined as a Function for which the values at the DOFs are assigned as f.x.array[:] = value. Here is the weak form for the problem that I am trying to solve (including already the boundary conditions, these are Robin BCs over all the boundaries).
- \int_{\mathcal{X}} |c_1|^2 \nabla m_1 \ \nabla v \ d \mathcal{X} + \int_{\partial \mathcal{X}} v (\frac{1-\alpha}{\alpha})b_1 \ dS + \int_{\partial \mathcal{X}} v (\frac{1-\alpha}{\alpha})m_1 \ dS - \int_{\mathcal{X}} c_1\cdot c_2 \nabla m_2 \ \nabla v \ d \mathcal{X} = - \int_{\mathcal{X}} \vec r_1\ \nabla v \ d \mathcal{X}

In this case, I am trying to solve for m_1 with the rest of coefficients and functions “fixed” or known. This also applies to the other function m_2 appearing in the expression.

For these additional functions I define them as:

self.V = functionspace(domain, ("Lagrange", 1))

self.m1_fem = TrialFunction(self.V)                               
self.m2_fem = TrialFunction(self.V)                               
self.test_v = TestFunction(self.V)                                
self.test_v_m2 = TestFunction(self.V)                             
                                                                  
self.c11 = dolfinx.fem.Function(self.V)                           
self.b1 = dolfinx.fem.Function(self.V)                            
self.c12 = dolfinx.fem.Function(self.V)                           
self.c22 = dolfinx.fem.Function(self.V)                           
self.b2 = dolfinx.fem.Function(self.V)                            
                                                                  
self.m2_prev = dolfinx.fem.Function(self.V)                       
self.m1_prev = dolfinx.fem.Function(self.V)                       
                                                                  
self.r12_comp = dolfinx.fem.Function(self.V)                      
self.r11_comp = dolfinx.fem.Function(self.V)                      
self.r13_comp = dolfinx.fem.Function(self.V)                      
                                                                  
self.r22_comp = dolfinx.fem.Function(self.V)                      
self.r21_comp = dolfinx.fem.Function(self.V)                      
self.r23_comp = dolfinx.fem.Function(self.V)                      
                                                                  
self.r1 = as_vector((self.r11_comp, self.r12_comp, self.r13_comp))
self.r2 = as_vector((self.r21_comp, self.r22_comp, self.r23_comp))

for which the values are just set as self.m2_prev.x.array[:] = value

Then this is how I have defined my UFL expression:

self.F = -self.c11*inner(grad(self.m1_fem), grad(self.test_v))*dx + ((1-self.alpha)/self.alpha) *inner(self.m1_fem, self.test_v) * ds + ((1-self.alpha)/self.alpha) * inner(self.b1, self.test_v) * ds - self.c12 * inner(grad(self.m2_prev), grad(self.test_v))*dx + inner(self.r1, grad(self.test_v))*dx                                                                                                                                            

From this you can see that I do self.c12 * inner(grad(self.m2_prev), grad(self.test_v))*dx.

Would this be fine in this case? Would the gradient of m2_prev make sense here or be well defined? Is it not an issue here as in the examples you were giving above for which the gradient is evaluated at the degree of freedom of Lagrange-1 elements?

I see here that this is also the same term applied to self.m1_fem. However, this is not a Function but my TrialFunction. I am not really sure if there is any difference here, can this grad operator be applied in the same way for both cases?

Thanks a lot for the feedback and help.

[dokken]

The example you have provided is a bit convoluted by not being reproducible, with loads of partially defined components. That being said, i will here give it a shot at trying to decipher what you want. Please correct me if I do not answer your question.

1. In your problem you have a known function f, which has been assigned some values (in some way).
2. You want to have grad(f) in your variational form.
3. You are wondering if this is fine to have in your variational formulation.

As far as I can tell, you have a term something * grad(f) * dx in your form. This is an ok term to have in your form, as dx is integrated per cell, and grad(f) is defined within every cell.

[kalosu]

Hi again @dokken,

Thanks for the answer. I understood it now that in this case this is fine since we are integrating over each cell via dx, so the fact that this grad(f) is not continuous on my vertices (degrees of freedom in my case) is not important.

In any case, I found that I can pre compute the gradient externally and then do:
inner(grad_vec, grad(self.test_v))*dx with grad_vec being a vector which entries correspond to the externally computed gradient at my DOF points.

In any case, thanks for the feedback.