I’m on modern Dolfinx version 0.10.0 running the nightly build.
The PDE being solved for is the shallow water equations
\textbf{u}_t + f(\hat{\textbf{k}}\times \textbf{u}) + g \nabla D = 0
D_t + H \nabla \cdot \textbf{u} = 0
on a spherical manifold immersed in a 3D space, where D is shallow layer depth, and \textbf{u} is the velocity, and H, g, and f are coefficients for height, gravity, and Coriolis, respectively. These two solutions can be used to yield the Kinetic and Potential energies of the system which should be conserved throughout (Total initial energy = Total final energy).
The mesh used is sphere_ico4 which can be found in this supplements file, and is an icosahedral meshed sphere, and the file solving this problem written in legacy Dolfin is linear-shallow-water.py. I attempted to adapt the code in this file to modern Dolfinx with the code below which is yielding unusual results
from mpi4py import MPI
import numpy as np
import ufl
import basix.ufl
import dolfinx as df
from petsc4py import PETSc
from dolfinx.fem import petsc
def initial_conditions(S, V):
u0 = df.fem.Function(S)
u0.interpolate(lambda x: np.zeros(x[:S.mesh.topology.dim].shape))
D0 = df.fem.Function(V)
D0.interpolate(lambda x: np.exp(-((-x[1]-1)/0.1)**2) )
return (u0, D0)
def energy(u, D, H, g):
kinetic = 0.5*H*ufl.dot(u,u)*ufl.dx # 0.5*H*dot(u, u)*dx
potential = 0.5*g*D*D*ufl.dx # 0.5*g*D*D*dx
return kinetic, potential
import meshio
tmp_data = meshio.dolfin.read("supplement/examples/mixed-poisson/hdiv-l2/meshes/sphere_ico4.xml")
mesh = df.mesh.create_mesh(
comm=MPI.COMM_WORLD,
cells=tmp_data.cells_dict["triangle"],
x=tmp_data.points,
e=ufl.Mesh(basix.ufl.element("Lagrange", "triangle", 1, shape=(3,))),
)
'''
Remove quotations to run code with custom spherical mesh
import gmsh
order = 1
res = 0.25
gmsh.initialize()
outer_sphere = gmsh.model.occ.addSphere(0, 0, 0, 1)
gmsh.model.occ.synchronize()
boundary = gmsh.model.getBoundary([(3, outer_sphere)], recursive=False)
gmsh.model.addPhysicalGroup(boundary[0][0], [boundary[0][1]], tag=1)
gmsh.option.setNumber("Mesh.CharacteristicLengthFactor", res)
gmsh.model.mesh.generate(2)
gmsh.model.mesh.setOrder(order)
mesh_data = df.io.gmshio.model_to_mesh(gmsh.model, MPI.COMM_WORLD, 0, gdim=3)
mesh = mesh_data.mesh
'''
x = ufl.SpatialCoordinate(mesh)
# mixed functionspace
S = df.fem.functionspace(mesh, ("RT", 1))
V = df.fem.functionspace(mesh, ("DG", 0))
W = ufl.MixedFunctionSpace(*(S, V))
u, D = ufl.TrialFunctions(W)
w, phi = ufl.TestFunctions(W)
# Set global orientation of test and trial vectors
global_orientation = ufl.sign(ufl.dot(x, ufl.CellNormal(mesh)))
u_ = global_orientation * u
w_ = global_orientation * w
# Setting up perp operator
k = ufl.CellNormal(mesh)
# Extract initial conditions
u_n, D_n = initial_conditions(S,V)
# Extract some parameters for discretization
dt = 0.05
f = x[2]
H = 1.0
g = 1.0
# Implicit midoint scheme discretization in time
u_mid = 0.5*(u_ + u_n)
D_mid = 0.5*(D + D_n)
# n x u_mid
u_perp = ufl.cross(k,u_mid)
# variational form
F = ufl.inner(u_ - u_n, w_)*ufl.dx
F -= dt*ufl.div(w_)*g*D_mid*ufl.dx
F += dt*f*ufl.inner(u_perp, w_)*ufl.dx
F += ufl.inner(D - D_n, phi)*ufl.dx
F += dt*H*ufl.div(u_mid)*phi*ufl.dx
a, L = ufl.system(F)
# Preassemble matrix (because we can)
A = ufl.extract_blocks(a)
# Define energy functional
kinetic_func, potential_func = energy(u_n, D_n, H, g)
# Setup solution function for current time
u_h = df.fem.Function(S)
D_h = df.fem.Function(V)
# Predefine b (for the sake of reuse of memory)
b = ufl.extract_blocks(L)
# Set-up linear solver (so that we can reuse LU)
petsc_options = {
"ksp_type": "preonly",
"pc_type": "lu",
"pc_factor_mat_solver_type": "mumps",
"ksp_error_if_not_converged": True,
}
problem = petsc.LinearProblem(
A,
b,
bcs=[],
u = [u_h,D_h],
petsc_options=petsc_options,
petsc_options_prefix="mixed_poisson_",
kind="mpi",
)
u_h, D_h = problem.solve()
# Set-up some time related variables
k = 0
t = 0.0
T = 10.0
# Output initial energy
E_k = mesh.comm.allreduce(df.fem.assemble_scalar(df.fem.form(kinetic_func)), op = MPI.SUM)
E_p = mesh.comm.allreduce(df.fem.assemble_scalar(df.fem.form(potential_func)), op = MPI.SUM)
print(t, E_k, E_p, E_k + E_p, D_n.x.petsc_vec.min(), D_n.x.petsc_vec.max())
Es = np.array([[t,E_k,E_p, E_k+E_p]])
# Primers
t = 0
k = 0
# Time Loop
while(t < (T - 0.5*dt)):
u_h, D_h = problem.solve()
# Update u_n
u_n.x.array[:] = u_h.x.array
# Update D_n
D_n.x.array[:] = D_h.x.array
# Update time and counter
t = np.round(t+dt,3)
k += 1
# Output current energy and max/min depth
E_k = mesh.comm.allreduce(df.fem.assemble_scalar(df.fem.form(kinetic_func)), op = MPI.SUM)
E_p = mesh.comm.allreduce(df.fem.assemble_scalar(df.fem.form(potential_func)), op = MPI.SUM)
Es = np.vstack((Es,[t,E_k,E_p,E_k+E_p]))
t = Es[:,0]
E_k = Es[:,1]
E_p = Es[:,2]
E_t = Es[:,3]
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot()
ax.plot(t,E_t,label = "$E_t$", color = 'purple')
ax.plot(t,E_k,label = "$E_k$", color = 'red')
ax.plot(t,E_p,label = "$E_p$", color = 'blue', linestyle = '--', linewidth = 0.5)
ax.set_ylim(0.0,0.20)
ax.set_ylabel("Energy")
ax.set_xlabel("$t$")
ax.legend()
ax.set_title("Energies obtained using sphere_ico4")
plt.show()
(I feel it’s important to mention that since this is a mixed problem where one of the solutions is a vector field, and we therefore opt to div-conforming space “RT”, and because of this, following this example handling a similar case (which modernizes the legacy Dolfin code in mixed-poisson-sphere.py in the same supplements file,) my code also includes global_orientation operating onto the vectors created in the RT space since (quoting Dokken here) “you have to encode the global orientation” when dealing with a RT space. That’s what this line does and why we use u_ and w_. This will also need to come back up again should I choose to plot the u_n vectors as their orientations will be off.)
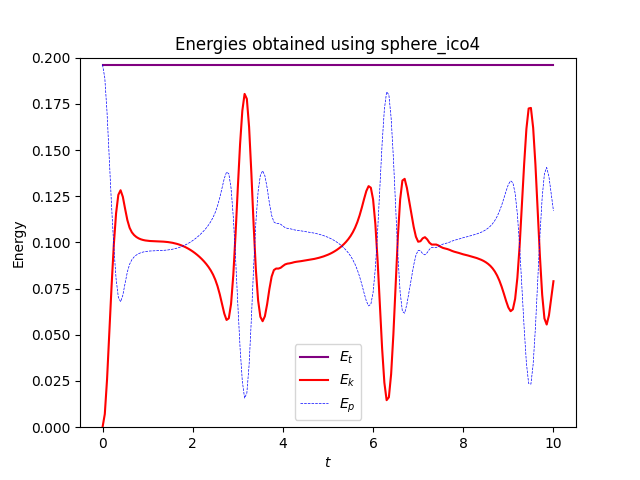
The plot should instead look exactly like this:
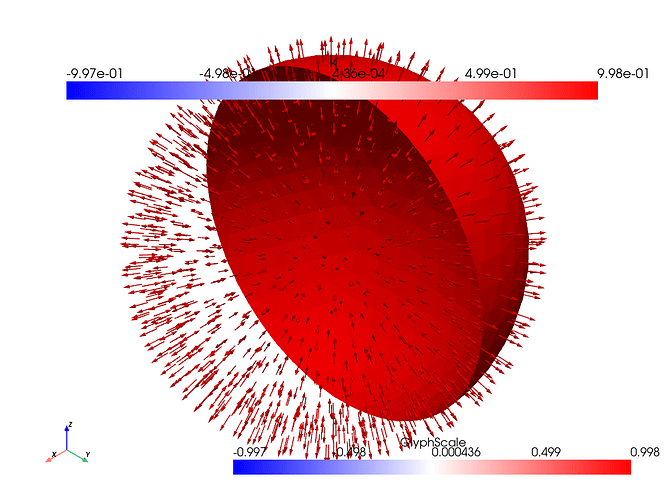
which are the results created from running the exact same code as above, but instead of the icosahdral spherical manifold, it uses a different spherical manifold which was generated in gmsh in the commented out code. I went ahead and plotted time evolutions of u and D (from an xz view) as well so see what might be happening


where it looks like they move forward for a frame before getting stuck for the remainder of time.
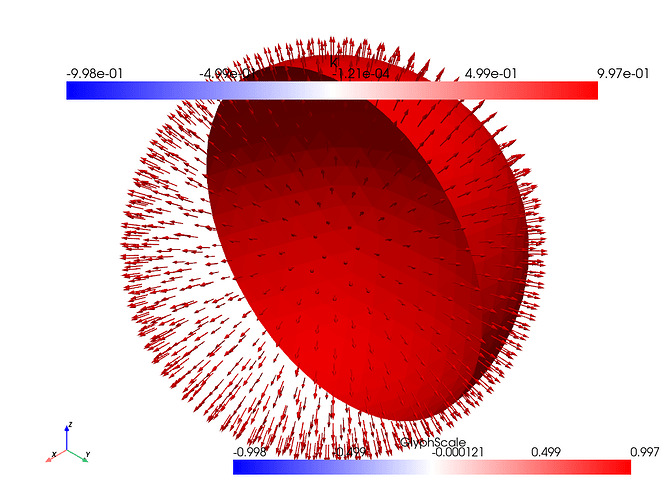
Here are what the solutions look like using the gmsh generated mesh instead


where they both evolve with time. I find it weird that the solution appears to bounce back and forth in the gifs and the energies plot rather than evolve and spread over the entire sphere, and the only thing I’ve changed between the cases was the mesh used. This issue persists with the other icosahedral meshes in the file which are simply different resolutions of the same mesh.