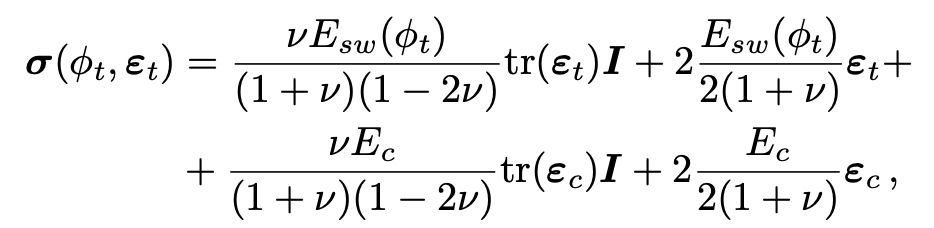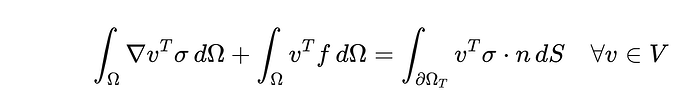Facing difficulty in solving modified elasticity equation for polymers difusion

[ishank_2210]

`E = 1.0
nu = 0.3
mu = E / (2.0 * (1.0 + nu))

Plane strain definition

lmbda = E * nu / ((1.0 + nu) * (1.0 - 2.0 * nu))

Plane stress definition

lmbda = 2 * mu * lmbda / (lmbda + 2 * mu)

Identity tensor

I = ufl.Identity(2)

Eigenstrain definition

epsilon_c_value = 0.62
epsilon_c = epsilon_c_value * I

def eps(u):
“”“Strain”“”
return ufl.sym(ufl.grad(u))

def sigma(u):
“”“Stress”“”
return 2.0 * mu * eps(u) + lmbda * ufl.tr(eps(u)) * ufl.Identity(2) +(nu * E / ((1 + nu) * (1 - 2 * nu))) * ufl.tr(epsilon_c) * ufl.Identity(2)+ (E/(1+nu))*epsilon_c

def a(u, v):
“”“The bilinear form of the weak formulation”“”
return ufl.inner(sigma(u), eps(v)) * dx

def L(v):
“”“The linear form of the weak formulation”“”
# Volume force
b = fem.Constant(msh, (0.0, 0.0))

# Surface force on the top
f = fem.Constant(msh, (0.0, 1.0))
return ufl.dot(b, v) * dx + ufl.dot(f, v) * ds(1)

%%

problem = fem.petsc.LinearProblem(
a(u, v), L(v), bcs=bcs, petsc_options={“ksp_type”: “preonly”, “pc_type”: “lu”}
)
uh = problem.solve()
uh.name = “displacement” `

I am getting this error

Adding expressions with non-matching form arguments () vs (‘v_1’,).

I guess because I am inputting Eigenstrain which makes my weak form non-bilinear, I am getting the error. So please someone can help me in setting the elasticity solver where the stress term can have eigenstrains. I don’t think simply linear solver will work. Any suggestions will be very helpful.

[dokken]

Please start by properly formatting the code and make sure it is reproducible. Note that if you write your variational form on residual form, ie, as a single form, you can split it into a bilinear and linear form with a, L = ufl.system(F)

[ishank_2210]

sure, thanks for the prompt reply.

[ishank_2210]

so, lets says my body force is zero and I don't have any traction force. So, I have only the first integral which is the inner product of test function with stress. My F in ufl.system(F) will be the first integral term right?

[dokken]

If sigma depends on your displacement u, there is no term on the rhs of your equation.

You can for instance see this in: Efficient usage of the Unified Form Language — FEniCS Tutorial @ Sorbonne

Please note that your initial post is still not properly formatted (using 3x` encapsulation), and is not reproducible.

[ishank_2210]

thanks a lot. I will upload my code and the problems that I am facing while solving cahn hilliard and elasticity equation simultaneously in proper format.