How to convert a vector of solution to function object?

1

Hello everyone,

I am trying to solve a heat conduction problem on 2 submeshes using mixed dimensional branch. However, I would like to use the lower level functions instead of using the high level solve function
solve (a == L, sol , bc)

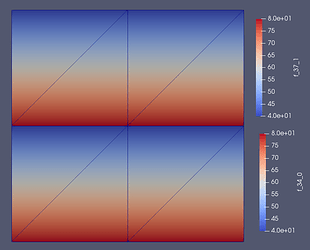
I have managed to solve the problem by create a new unknown vector and store the solution in that vector (The solution seems to be correct compared to the solution from the high level solve function visulised in ParaView).

Solution from high level solve function

temp
temp785×632 28.9 KB

Solution from low level solve function
x

However, I also need to convert this solution vector back to Function object inorder to visualize the result in ParaView.

Could anyone please suggest how to perform this conversion?

Here is the MWE

from __future__ import print_function
import numpy as np
import matplotlib.pyplot as plt
from dolfin import *
from ufl.algorithms import expand_derivatives
import petsc4py.PETSc as petsc

class Top(SubDomain):
    def inside(self, x, on_boundary):
        return near(x[1], 1.0)

class Left1(SubDomain):
   def inside(self, x, on_boundary):
        return near(x[0], 0.0) and between(x[1], (0.5, 1))

class Right1(SubDomain):
    def inside(self, x, on_boundary):
        return near(x[0], 1.0) and between(x[1], (0.5, 1))

class Interface(SubDomain):
    def inside(self, x, on_boundary):
        return near(x[1], 0.5)

class Left2(SubDomain):
    def inside(self, x, on_boundary):
        return near(x[0], 0.0) and between(x[1], (0.0, 0.5))

class Right2(SubDomain):
    def inside(self, x, on_boundary):
        return near(x[0], 1.0) and between(x[1], (0.0, 0.5))     
    
class Bottom(SubDomain):
    def inside(self, x, on_boundary):
        return near(x[1], 0.0)
    
# Create meshes
mesh = UnitSquareMesh(2, 2)

# Domain markers
domain = MeshFunction("size_t", mesh, mesh.geometry().dim(), 0)

for c in cells(mesh):
  domain[c] = c.midpoint().y() > 0.5

# Interface markers
facets = MeshFunction("size_t", mesh, mesh.geometry().dim()-1, 0)
Interface().mark(facets,1)
  
# Define submeshes
mesh_F = MeshView.create(domain, 1)
mesh_S = MeshView.create(domain, 0)

# Function spaces
TE = FiniteElement("CG", mesh.ufl_cell(), 1)   # Temperature
T_F  = FunctionSpace(mesh_F,TE)    # Temperature on the upper domain
T_S  = FunctionSpace(mesh_S,TE)    # Temperature on the lower domain
W = MixedFunctionSpace(T_F, T_S)

# Markers for Dirichlet and Neuman bcs
ff_F = MeshFunction("size_t", mesh_F, mesh_F.geometry().dim()-1, 0)
Top().mark(ff_F, 1)
Left1().mark(ff_F, 2)
Right1().mark(ff_F, 3)
Interface().mark(ff_F, 4)

ff_S = MeshFunction("size_t", mesh_S, mesh_S.geometry().dim()-1, 0)
Interface().mark(ff_S, 5)
Left2().mark(ff_S, 6)
Right2().mark(ff_S, 7)
Bottom().mark(ff_S, 8)

# Boundary conditions
bc_U1 = DirichletBC(W.sub_space(0), Constant(40), ff_F, 1)
bc_U2 = DirichletBC(W.sub_space(0), Constant(80), ff_F, 4)
bc_L1 = DirichletBC(W.sub_space(1), Constant(40), ff_S, 5)
bc_L2 = DirichletBC(W.sub_space(1), Constant(80), ff_S, 8)
bcs = [bc_U1, bc_U2, bc_L1, bc_L2]

# Material parameters
k_f = Constant(227) #Constant(0.5984) 
k_s = Constant(0.5984) #Constant(227)

# Measures 
dx_F  = Measure("dx", domain=W.sub_space(0).mesh())
ds_F  = Measure("ds", domain=W.sub_space(0).mesh(), subdomain_data=ff_F)
dx_S  = Measure("dx", domain=W.sub_space(1).mesh())
ds_S  = Measure("ds", domain=W.sub_space(1).mesh(), subdomain_data=ff_S)

nf = FacetNormal(mesh_F) # unit normal vector on the surfaces of the fluid mesh
ns = FacetNormal(mesh_S) # unit normal vector on the surfaces of the solid mesh

(tf, ts) = TrialFunctions(W)
(zf, zs) = TestFunctions(W)

# Define the weak form
f = Constant(0.0)

# Variational problem in fluid
a_fluid = k_f*inner(grad(tf), grad(zf))*dx_F
L_fluid = f*zf*dx_F

# Variational problem in solid
a_solid = k_s*inner(grad(ts), grad(zs))*dx_S
L_solid = f*zs*dx_S

# Combined variational problem
a =  a_fluid + a_solid
L =  L_fluid + L_solid

# Define function object
t_mixed = Function(W)
tf = t_mixed.sub(0)
ts = t_mixed.sub(1)

# Assembly and Solve
system = assemble_mixed_system(a == L, t_mixed, bcs) 
matrix_blocks = system[0]
rhs_blocks = system[1]

A = PETScNestMatrix(matrix_blocks)
b = Vector()
A.init_vectors(b, rhs_blocks)
A.convert_to_aij()

x = Vector()
solve(A,x,b)

Thank you very much
Phuris

2

Hi,

Knowing the function space, you should be able to create a function with the vertex values like the usual case, no?

unew = Function(tf.function_space(), x)

assuming x[:] contains the values you want to assign the dofs of a new function.

1 Like
3

Couldnt you just use the vector from a function of the appropriate function space?

u=Function(W)
b=u.vector()

Then solve the problem with b and then write u to file.

2 Likes
4

I try the following,

x = t_mixed.vector()
solve(A,x,b)

But I got the error

Exception has occurred: AttributeError
'Function' object has no attribute '_cpp_object'
5

Thank you for you suggestion.

It does assign some value to the tf when I try unew = Function(tf.function_space(), x), but the result doesn’t seem right. I got the following

Capture
Capture971×487 10.7 KB

Maybe the function need to be modified somehow to comply with the mixed-dimensional problem.

6

If you are solving the problem correctly then it shouldn’t happen. If I copy your code as is with

unew = Function(tf.function_space(), x)

I get this:
garbage

Edit: I didn’t properly see the original figure. You can use @dokken 's trick above along with setting the dofs located at the corresponding coordinate. These should be accessible using W.sub_space(0).tabulate_dof_coordinates() and likewise.

Edit 2: As a quick example consider

tf.vector()[:] = x[:len(tf.vector())]
ts.vector()[:] = x[len(tf.vector()):]
plt.figure()
p1 = plot(tf, cmap=plt.cm.jet)
p2 = plot(ts, cmap=plt.cm.jet)
plot(mesh)
plt.colorbar(p1)

Just make sure to cross check the dof coordinates once again, to avoid any errors in setting the vertex values.
garbage

2 Likes
7

When doing solve(A,x,b), x will be a vector with the size of your product space T_F x T_S (= T_F.dim() + T_S.dim()). You then need to split it, as you would do with t_mixed.sub(0) and t_mixed.sub(1) with a Function t_mixed = Function(W), but with a Vector() type.
You can extract the values manually using x.get_local() and the appropriate indices, to fill the Functions you want to export :

x0 = Function(T_F)
x0.vector().set_local(x.get_local()[:T_F.dim()])
x0.vector().apply("insert")

and

x1 = Function(T_S)
x1.vector().set_local(x.get_local()[T_F.dim():])
x1.vector().apply("insert")
3 Likes
8

Thank you for this. I get the same result as using the high slevel solve function now.

9

Does the x0.vector().set_local(x.get_local()[:T_F.dim(),T_S.dim():]) mean that the location of the dof coordinate of the entry in x from the first entry to the [T_F.dim()] entry is assign to x0 ?
What if I have 3 spaces for the solution (e.g. T_F, T_M, T_S), can x0.vector().set_local(x.get_local()[:T_F.dim() T_S.dim():]) do the job?

10

First of all, the command you suggest would not make sense here since x is a 1-dimensional array.
x contains the vectors associated with each spaces, i.e. if W = T_1 x T_2 x … x T_N, then x would be on the form x = [x0, x1, …, x_n] with xi \in T_i

With three spaces you would split x into three functions x0, x1 and x2.
The vector x will have the size of the product space : T_F.dim() + T_M.dim() + T_S.dim()
The part of x belonging to T_F (say x0) corresponds to indices from 0 to T_F.dim() : [:T_F.dim()]
The part of x belonging to T_M (say x1) corresponds to indices from T_F.dim() to T_F.dim() + T_M.dim() : [T_F.dim():T_F.dim() + T_M.dim()]
The part of x belonging to T_S (say x2) corresponds to indices from T_F.dim() + T_M.dim() to the end of the vector : [T_F.dim() + T_M.dim():]

x0.vector().set_local(x.get_local()[:T_F.dim()]
x1.vector().set_local(x.get_local()[T_F.dim():T_F.dim() + T_M.dim()]
x2.vector().set_local(x.get_local()[T_F.dim() + T_M.dim():]
1 Like
11

Thanks again for your help :grin: