How to get adjoint solution from compute_gradient()

dolfin-adjoint
1

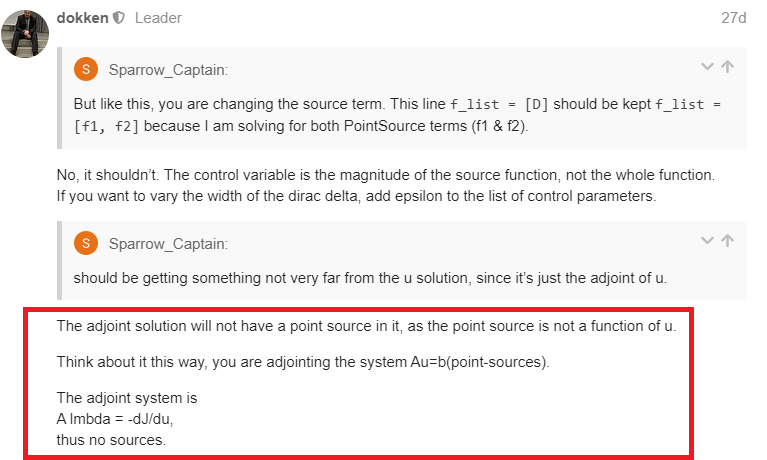
Hello, I would like to be able to access the adjoint variable (solution of the adjoint system).

I calculate the gradient \frac{dJ}{dm} by using the command compute_gradient(J, m). I’m assuming that the gradient calculation is done using the adjoint approach, so following the notation in the dolfin-adjoint mathematical background of adjoints, the adjoint equation is solved (\frac{\partial F(u,m)}{\partial u})^* \lambda=\frac{\partial J}{\partial u}^* and the result is used to calculate \frac{dJ}{dm}^* = -\frac{\partial F}{\partial m}^* \lambda + \frac{\partial J}{\partial m}^*. I’d like to be able to get the variable \lambda.

I’ve tried using J.block_variable.adj_value, but I’m not sure that I’m using it correctly because I get back a value of 1, when it should be a vector.

In this simple example, I’m using dolfin-adjoint 2019.1.0 and solving a linear elasticity pde.

from fenics import *
from fenics_adjoint import *
import numpy as np
from ufl import nabla_div

# Define parameters
nelx = 30
nely = 15
nelz = 15
lx = float(nelx)
ly = float(nely)
lz = float(nelz)
E = 1
v = 0.3
mu = Constant(E / (2*(1+v)))
lmbda = Constant(E*v / ((1+v)*(1-2*v)))

# Create a mesh
mesh = BoxMesh.create(
    [Point(0.0, 0.0, 0.0), Point(lx, ly, lz)], # define opposing corners
    [nelx, nely, nelz], # number of elements in each direction
    CellType.Type.hexahedron)
mesh = Mesh(mesh)

# FE function space and functions
V = VectorFunctionSpace(mesh, "CG", 1)
D = FunctionSpace(mesh, "DG", 0)
u = TrialFunction(V)
v = TestFunction(V)
u_sol = Function(V) # function for storing the solution
density = Function(D) # density field

# Bounday condition
class Left(SubDomain):
    def inside(self, x, on_boundary):
        return near(x[0], 0.)
left = Left()
bc = DirichletBC(V, Constant((0., 0., 0.)), left)

# Stress and strain functions
def sigma(u):
    n = len(u) # size of u
    return lmbda*nabla_div(u)*Identity(n) + 2*mu*epsilon(u)

def epsilon(u):
    return 0.5*(nabla_grad(u) + nabla_grad(u).T)

# Define density field
density.vector()[:] = np.ones(nelx*nely*nelz)

# Define forms
f = Constant((0., 0., -1.))
L = dot(f, v) * dx
a = inner(density*sigma(u), nabla_grad(v)) * dx

# Solve
A, b = assemble_system(a, L, bc)
solver = KrylovSolver("cg", "ilu")
solver.solve(A, u_sol.vector(), b)

# Get derivative
J = assemble(action(L, u_sol)) # define compliance
m = Control(density) # define density as the design variable
dJ_dm = compute_gradient(J, m)

# Get adjoint solution
adjoint_sol = J.block_variable.adj_value
print(type(adjoint_sol))
print('adjoint value:', adjoint_sol)
2

As each block has an adjoint (not just the solve block), you need to access the correct one.
I think you want:

print(u_sol.block_variable.adj_value[:])
3

Thank you so much. I do think that is the adjoint I want, however, I am a bit surprised by the result.

The function J that I’m using is actually self-adjoint, so if you calculate \frac{dJ}{dm} using the adjoint approach you’d find that \lambda=-u where u is the solution to the pde. However, the values that I get from u_sol.block_variable.adj_value[:] are quite different than the solution values u_sol.vector()[:]. Do you have any idea why this discrepancy would be occuring?

4

Shouldn’t you actually get that \lambda=u
as J=\int_\Omega f \cdot u \mathrm{d} x , thus \frac{\partial J}{\partial u}[v]=\int_{\Omega} f\cdot v~\mathrm{dx} which is equal to the LHS of your original problem?
To get this, you can add the following code:

tape = get_working_tape()
solve_block = tape.get_blocks()[1]
print(solve_block.adj_sol.vector()[:])
5

Yes, you’re right, it should be that \lambda = u. The negative sign was my mistake.

Thank you so much for your help, that last bit of code did the trick.

7

What version of dolfin, dolfin-adjoint and pyadjoint are you using?

8

image

9

Maybe I need to install a depricated version of those 3 lib ?

10

I cannot reproduce the issue with quay.io/fenicsproject/stable:latest (dolfin 2019.1.0)
and dolfin_adjoint 2023.0.0 (same version for pyadjoint).
It can also not be reproduced with ghcr.io/scientificcomputing/fenics:2023-04-21 which is a slightly more up to date version of dolfin than 2019.1.0 (it includes patches up to 21.04.2023).
Please copy-paste the complete code that you are running into a post with 3x` encapsulation, i.e.

```python
# add code here
```

and add the full stack trace in similar encapsulation

```bash
add stack trace here
```
12

Hello @dokken,

I have a question on a point you said once.

image
image767×460 25.7 KB

In the dolfin-adjoint mathematical background of adjoints we can see that ∂J/∂u is the source term, which is included in the λ (the adjoint variable associated with u).

Does this mean that in the adjoint solution, we should see the effect of the sources ?

13

You will see some influence of the sources, as you end up with using a rhs that depend on the point source, but it isn’t equivalent to the rhs being a point source.

1 Like
14

a rhs that depend on the point source

You mean ∂J/∂u, right ?

isn’t equivalent to the rhs being a point source

You mean that : ∂J/∂u ≠ source term f, right ?

Conclusion : There is no point of asking if we can get the ∂J/∂u values, since they do not represent the adjoint of the source term f.

Thank you for the time.

15

If your J is \int_\Omega f \cdot u~\mathrm{dx}

then \frac{\partial J}{\partial u}[\delta u]= \int_\Omega f \cdot \delta u ~ \mathrm{d}x.
Thus if f is your point-source, then it will be reflected in dJ/du.

1 Like
16

But if J doesn’t include f ? i.e :

image

Then in compute_gradient, we pass the source term f as a control parameter, and this is why we see a reflection of the source term in ∂J/∂u ?

PS : Maybe I am confused because f in carolina_jauregui example is a force per unit of volume (elasticity pde), and I am trying to do an analogy with poisson pde problem where f is a source term ?

17

As you correctly summarizes, the problem depends on how you define J. It is easy to compute dJ/du in your case as well, and there you will see that the point sources do not explicitly appear in the variational form.

1 Like
18

Thank you, it’s clear for me now :slight_smile: !