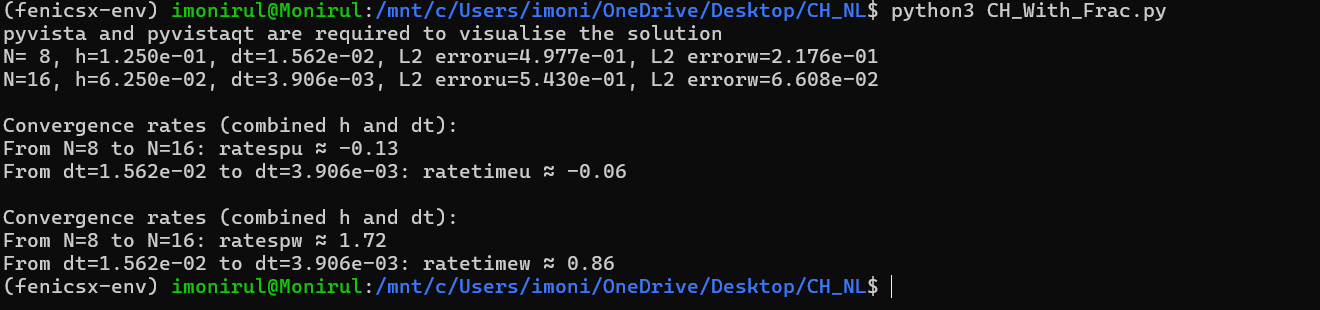
Hello, everyone, I am trying to implement the ideas in mixed-poisson demo code
in the nonlinear Cahn-Hilliard Equation. I am wondering with results. I have used fixed point method for the nonlinearity. error is coming nan after first level.
Here, is my code>>
import os
try:
from petsc4py import PETSc
import dolfinx
if not dolfinx.has_petsc:
print("This demo requires DOLFINx to be compiled with PETSc enabled.")
exit(0)
except ModuleNotFoundError:
print("This demo requires petsc4py.")
exit(0)
from mpi4py import MPI
import numpy as np
import ufl
from basix.ufl import element, mixed_element
from dolfinx import default_real_type, log, plot
from dolfinx.fem import Function, functionspace
from dolfinx.fem.petsc import LinearProblem
from dolfinx.io import XDMFFile
from dolfinx.mesh import CellType, create_unit_square
from dolfinx import mesh, fem, io
from ufl import Measure, SpatialCoordinate, TestFunctions, TrialFunctions, div, exp, inner, grad
try:
import pyvista as pv
import pyvistaqt as pvqt
have_pyvista = True
if pv.OFF_SCREEN:
pv.start_xvfb(wait=0.5)
except ModuleNotFoundError:
print("pyvista and pyvistaqt are required to visualise the solution")
have_pyvista = False
# Save all logging to file
#log.set_output_file("log.txt")
def run_simulation(N, dt, T=1.0, degree=1, max_fp_iter=10, fp_tol=1e-6,p=0.1):
#msh = create_unit_square(MPI.COMM_WORLD, N, N, CellType.quadrilateral)
msh = create_unit_square(MPI.COMM_WORLD, N, N, CellType.quadrilateral)
P1 = element("Lagrange", msh.basix_cell(), 1, dtype=default_real_type)
ME = functionspace(msh, mixed_element([P1, P1]))
V = functionspace(msh, P1)
# Test and trial functions for the mixed space
u, w = ufl.TrialFunctions(ME)
phi, psi = ufl.TestFunctions(ME)
x = SpatialCoordinate(msh)
dx = Measure("dx", msh)
class exact_solution_u:
def __init__(self, t):
self.t = t
def __call__(self, x):
return np.exp(np.cos(self.t)) * np.cos(np.pi * x[0]) * np.cos(np.pi * x[1])
class exact_solution_w:
def __init__(self,t):
self.t = t
self.p = p # Assuming p is a parameter needed for the solution
def __call__(self, x):
return ((np.exp(np.cos(self.t)) *np.cos(np.pi * x[0])* np.cos(np.pi * x[1]))**3
-(np.exp(np.cos(self.t)) *np.cos(np.pi * x[0])* np.cos(np.pi * x[1]))
+2*(np.pi**2)*self.p*(np.exp(np.cos(self.t)) *np.cos(np.pi * x[0])* np.cos(np.pi * x[1])))
def f_expr(x,t):
return (np.cos(np.pi*x[0])*np.cos(np.pi*x[1])*np.exp(np.cos(t))*(-np.sin(t))
- 6*(np.pi)**2*np.exp(3*np.cos(t))*(np.cos(np.pi*x[0])*((np.sin(np.pi*x[0]))**2)*(np.cos(np.pi*x[1]))**3
+ np.cos(np.pi*x[1])*((np.sin(np.pi*x[1]))**2)*(np.cos(np.pi*x[0]))**3)
+ 6*(np.pi)**2*np.exp(3*np.cos(t))*(np.cos(np.pi*x[0])*np.cos(np.pi*x[1]))**3
+ (4*(np.pi)**4*p - 2*(np.pi)**2)*np.cos(np.pi*x[0])*np.cos(np.pi*x[1])*np.exp(np.cos(t)))
f = fem.Function(V)
t = 0
u_exact = exact_solution_u(t)
w_exact = exact_solution_w(t)
# Initial conditions
u_n = fem.Function(V)
u_n.interpolate(u_exact)
w_n = fem.Function(V)
w_n.interpolate(w_exact)
# Solution functions
vh = fem.Function(ME)
uh, wh = vh.split()
uk = fem.Function(V) # For fixed-point iteration
# Define prime_func here (right after defining V)
prime_func = fem.Function(V) # <-- ADD THIS LINE
# Add stabilization parameter calculation
stab = fem.Constant(msh, default_real_type(0.0)) # Initial stabilization
# Time stepping
num_steps = int(T / dt)
for n in range(num_steps):
t += dt
u_exact.t = t
w_exact.t = t
#f.interpolate(f_expr)
# Update source term f with current time
f.interpolate(lambda x: f_expr(x, t+dt/2)) # Pass current time to f_expr
uk.interpolate(u_n) # Initialize with previous solution
# Compute stabilization using current uk
# Compute stabilization parameter
prime_func.interpolate(lambda x: 3.0 * uk.x.array**2 - 1.0)
max_prime = msh.comm.allreduce(np.max(prime_func.x.array), op=MPI.MAX)
stab.value = max(max_prime, 1.0)
for k in range(max_fp_iter):
# Bilinear form
a = (inner(u,phi)*dx
+ dt*inner(grad(w), grad(phi))*dx
+ inner(w,psi)* dx
- p*dt*inner(grad(u), grad(psi))*dx
- stab*inner(u, psi)*dx # Stabilization term
)
# Linear form
L = (inner((u_n+ dt*f),phi)*dx
+ inner((uk**3 - uk - stab*uk), psi)*dx # Stabilized nonlinear term
)
# Solve the linearized system
problem = LinearProblem(
a, L,
petsc_options={
"ksp_type": "preonly",
"pc_type": "lu",
"pc_factor_mat_solver_type": "superlu_dist",
},
)
vh = problem.solve()
uh, wh = vh.split()
# Compute fixed-point error
fp_error_u = np.sqrt(msh.comm.allreduce(
fem.assemble_scalar(fem.form(inner((uh - uk),(uh - uk))*dx)), op=MPI.SUM))
if MPI.COMM_WORLD.rank == 0:
print(f" FP iter {k}: error = {fp_error_u:.3e}")
if fp_error_u < fp_tol:
break
uk.interpolate(uh) # Update for next iteration
# Update for next iteration
u_n.interpolate(uh)
w_n.interpolate(wh)
# Save solution
with io.XDMFFile(MPI.COMM_WORLD, "solution.xdmf", "w") as xdmf:
xdmf.write_mesh(msh)
xdmf.write_function(uh, t)
xdmf.write_function(wh, t)
# Error computation
V_ex = fem.functionspace(msh, ("Lagrange", degree + 1))
u_ex = fem.Function(V_ex)
w_ex = fem.Function(V_ex)
u_ex.interpolate(u_exact)
w_ex.interpolate(w_exact)
erroru = np.sqrt(msh.comm.allreduce(
fem.assemble_scalar(fem.form(inner((uh - u_ex),(uh - u_ex))*dx)), op=MPI.SUM))
errorw = np.sqrt(msh.comm.allreduce(
fem.assemble_scalar(fem.form(inner((wh - w_ex),(wh - w_ex))*dx)), op=MPI.SUM))
h = 1.0 / N
return h, dt, erroru, errorw
if __name__ == "__main__":
Ns = [8,16,32,64]
hs, dts, errorsu, errorsw = [], [], [], []
for N in Ns:
h = 1.0 / N
dt = h**2
h_val, dt_val, erroru, errorw = run_simulation(N, dt)
hs.append(h_val)
dts.append(dt_val)
errorsu.append(erroru)
errorsw.append(errorw)
if MPI.COMM_WORLD.rank == 0:
print(f"N={N:2d}, h={h_val:.3e}, dt={dt_val:.3e}, L2 erroru={erroru:.3e}, L2 errorw={errorw:.3e}")
# Compute convergence rate of u
if MPI.COMM_WORLD.rank == 0:
print("\nConvergence rates (combined h and dt):")
for i in range(1, len(errorsu)):
ratespu = np.log(errorsu[i-1] / errorsu[i]) / np.log(hs[i-1] / hs[i])
print(f"From N={Ns[i-1]} to N={Ns[i]}: ratespu ≈ {ratespu:.2f}")
ratetimeu = np.log(errorsu[i-1] / errorsu[i]) / np.log(dts[i-1] / dts[i])
print(f"From dt={dts[i-1]:.3e} to dt={dts[i]:.3e}: ratetimeu ≈ {ratetimeu:.2f}")
# Compute convergence rate of w
if MPI.COMM_WORLD.rank == 0:
print("\nConvergence rates (combined h and dt):")
for i in range(1, len(errorsw)):
ratespw = np.log(errorsw[i-1] / errorsw[i]) / np.log(hs[i-1] / hs[i])
print(f"From N={Ns[i-1]} to N={Ns[i]}: ratespw ≈ {ratespw:.2f}")
ratetimew = np.log(errorsw[i-1] / errorsw[i]) / np.log(dts[i-1] / dts[i])
print(f"From dt={dts[i-1]:.3e} to dt={dts[i]:.3e}: ratetimew ≈ {ratetimew:.2f}")
yeilding
Please help to fix this errors in my above code.
Thanks in advance!.