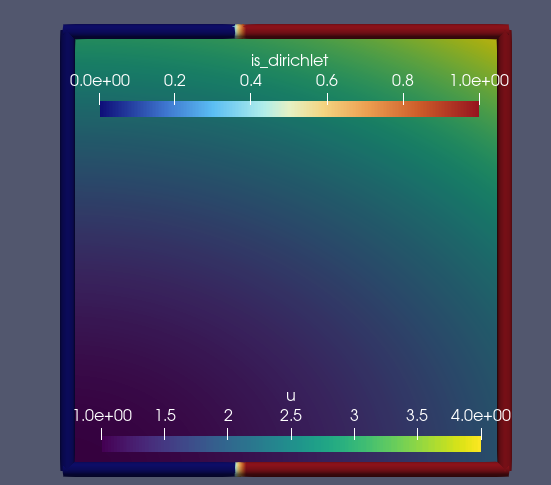
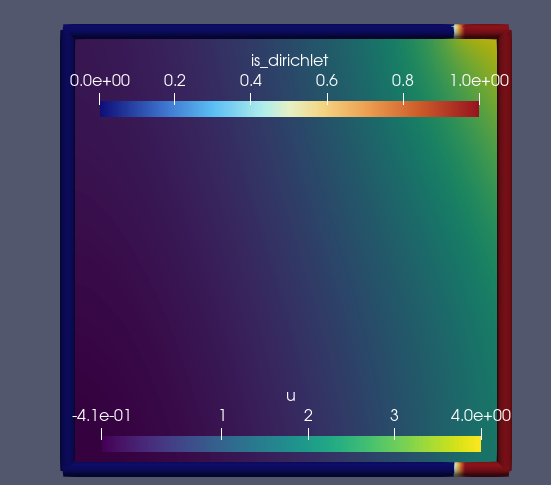
You don’t need to generate the weak forms again at each time step, but you would need to modify the list of boundary conditions on each time step.
Here is an illustration using an indicator function:
# # Ilustration of varying boundary conditions through physical parameters
# Author: Jørgen S. Dokken <dokken@simula.no>
# SPDX-License-Identifier: MIT
from mpi4py import MPI
import dolfinx.fem.petsc
import ufl
import numpy as np
comm = MPI.COMM_WORLD
N = 40
mesh = dolfinx.mesh.create_unit_square(comm, N, N)
V = dolfinx.fem.functionspace(mesh, ("Lagrange", 1))
u, v = ufl.TrialFunction(V), ufl.TestFunction(V)
uh = dolfinx.fem.Function(V, name="u")
mesh.topology.create_connectivity(mesh.topology.dim - 1, mesh.topology.dim)
exterior_facets = dolfinx.mesh.exterior_facet_indices(mesh.topology)
facet_mesh, entity_map = dolfinx.mesh.create_submesh(
mesh, mesh.topology.dim - 1, exterior_facets
)[:2]
Q = dolfinx.fem.functionspace(facet_mesh, ("Lagrange", 1))
# Create an initial split of the boundary
indicator = dolfinx.fem.Function(Q, name="indicator")
indicator.interpolate(lambda x: x[0] + 0.6)
is_dirichlet = ufl.conditional(ufl.ge(indicator, 1.0), 1, 0)
# Define an analytical solution to enforce bcs
uD = dolfinx.fem.Function(V)
x = ufl.SpatialCoordinate(mesh)
u_ex = 1 + x[0] ** 2 + 2 * x[1] ** 2
uD.interpolate(dolfinx.fem.Expression(u_ex, V.element.interpolation_points))
f = -ufl.div(ufl.grad(u_ex))
n = ufl.FacetNormal(mesh)
g = -ufl.dot(ufl.grad(u_ex), n)
dx = ufl.dx(domain=mesh)
ds = ufl.ds(domain=mesh)
F = ufl.inner(ufl.grad(u), ufl.grad(v)) * dx
F -= f * v * dx
F += (1 - is_dirichlet) * g * v * ds
h = 2 * ufl.Circumradius(mesh)
alpha = dolfinx.fem.Constant(mesh, dolfinx.default_scalar_type(10))
F += -is_dirichlet * ufl.inner(n, ufl.grad(u)) * v * ds
F += (
-is_dirichlet * ufl.inner(n, ufl.grad(v)) * (u - uD) * ds
+ is_dirichlet * alpha / h * ufl.inner(u - uD, v) * ds
)
a, L = ufl.system(F)
problem = dolfinx.fem.petsc.LinearProblem(
a,
L,
bcs=[],
petsc_options={
"ksp_type": "preonly",
"pc_type": "lu",
"pc_factor_mat_solver_type": "mumps",
"ksp_error_if_not_converged": True,
},
u=uh,
entity_maps=[entity_map],
petsc_options_prefix="mwe_",
)
problem.solve()
vtx_u = dolfinx.io.VTXWriter(comm, "u.bp", [uh])
vtx_u.write(0.0)
is_dirichlet_func = dolfinx.fem.Function(Q, name="is_dirichlet")
is_dirichlet_expr = dolfinx.fem.Expression(is_dirichlet, Q.element.interpolation_points)
is_dirichlet_func.interpolate(is_dirichlet_expr)
vtx_id = dolfinx.io.VTXWriter(comm, "id.bp", [indicator, is_dirichlet_func])
vtx_id.write(0.0)
L2_u = dolfinx.fem.form(ufl.inner(uh - u_ex, uh - u_ex) * dx)
L2_local = dolfinx.fem.assemble_scalar(L2_u)
L2_u_global = np.sqrt(comm.allreduce(L2_local, op=MPI.SUM))
print(f"L2 error: {L2_u_global:.6e}")
is_dirichlet_area = dolfinx.fem.form(is_dirichlet * ds, entity_maps=[entity_map])
print(
"Dirichlet area",
comm.allreduce(dolfinx.fem.assemble_scalar(is_dirichlet_area), op=MPI.SUM),
)
indicator.interpolate(lambda x: x[0] + 0.1)
print(
"Dirichlet area post change",
comm.allreduce(dolfinx.fem.assemble_scalar(is_dirichlet_area), op=MPI.SUM),
)
problem.solve()
L2_local = dolfinx.fem.assemble_scalar(L2_u)
L2_u_global = np.sqrt(comm.allreduce(L2_local, op=MPI.SUM))
print(f"L2 error: {L2_u_global:.6e}")
is_dirichlet_func.interpolate(is_dirichlet_expr)
vtx_u.write(1.0)
vtx_id.write(1.0)
vtx_u.close()
vtx_id.close()
First time solving:
After update
Of course, if we now use a
g that is different than the analytical g, we will clearly see the effect on the solution. For instance, using: g = ufl.sin(x[0]) * ufl.cos(x[1] * ufl.pi):