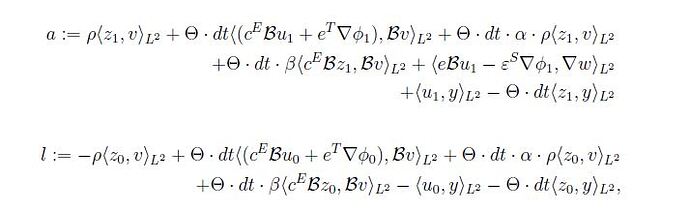Good evening drokken,
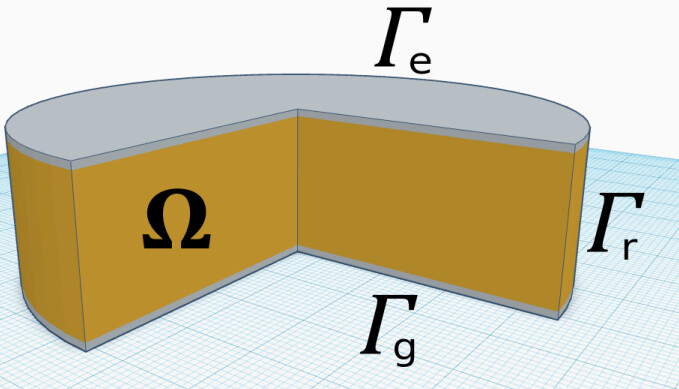
please I would like to know if you can give me some indications how to solve this problem because I think I have solved all the errors and the code runs without error but the output does not receive any voltage although I have applied a value of -0.00098462 Volt on the upper side but the result is unchanged.
from fenics import *
from mshr import *
import numpy as np
from math import *
from matplotlib import pyplot as plt
from dolfin import *
import matplotlib.cm as cm
import matplotlib.tri as tri
from mpl_toolkits.axes_grid1 import make_axes_locatable
import ufl
c_11 = 1.19e11
c_12 = 0.84e11
c_13 = 0.83e11
c_33 = 1.17e11
c_44 = 0.21e11
eps_11 = 8.15e-9
eps_33 = 6.58e-9
e_15 = 12.09
e_13 = -6.03
e_33 = 15.49
alpha = 1.267e5
beta = 6.259e-10
theta = 0.5
rho_Piezo = Constant(7700.0)
# different tensor of material
# Elasticity tensor c^E
C = as_tensor(
[
[c_11, c_12, c_13, 0.0, 0.0, 0.0],
[c_12, c_11, c_13, 0.0, 0.0, 0.0],
[c_13, c_13, c_33, 0.0, 0.0, 0.0],
[0.0, 0.0, 0.0, c_44, 0.0, 0],
[0.0, 0.0, 0.0, 0.0, c_44, 0.0],
[0.0, 0.0, 0.0, 0.0, 0.0, (c_11 - c_12) / 2],
]
)
# coupling tensor e
E_piezo = as_tensor(
[
[0.0, 0.0, 0.0, 0.0, e_15, 0.0],
[0.0, 0.0, 0.0, e_15, 0.0, 0.0],
[e_13, e_13, e_33, 0.0, 0.0, 0.0],
]
)
# transpose form tensor
E_t_piezo = as_tensor(
[
[0.0, 0.0, e_13],
[0.0, 0.0, e_13],
[0.0, 0.0, e_33],
[0.0, e_15, 0.0],
[e_15, 0.0, 0.0],
[0.0, 0.0, 0.0],
]
)
# Permittivitatstensor epsilon^S
Eps_s = as_tensor([[eps_11, 0.0, 0.0], [0.0, eps_11, 0.0], [0.0, 0.0, eps_33]])
# Setup mesh
resolution = 10
geometry = Cylinder(Point(0, 0, 0), Point(0, 0, 0.001), 0.005, 0.005)
# Making Mesh (30 corresponds to the mesh density)
mesh = generate_mesh(geometry, resolution)
# --------------------
# Functions and classes
# --------------------
V = VectorElement("CG", mesh.ufl_cell(), 2, dim=3)
W = FiniteElement("CG", mesh.ufl_cell(), 1)
M = FunctionSpace(mesh, MixedElement([V, V, W]))
# Get the needed boundaries:
# 1. To apply a predefined stress on it We keep it simple: the top face sees the same stress vector.
# 2. For zero Displacement we choose the bottom face of the disc
class TopBoundary(SubDomain):
def inside(self, x, on_boundary):
return on_boundary and near(x[2], 0.001)
class BottomBoundary(SubDomain):
def inside(self, x, on_boundary):
return on_boundary and near(x[2], 0.0)
# first define the function for the strain tensor in fenics notation
# definition of the different components of my Stress tensor equation (sigma=C^E:Bu-e_transpose.E)
# rewrite the tensor into a vector using Voigt notation
def strain3voigt(ten):
# FEniCS does not know anything about Voigt notation,
# so one need to access the components directly as eps[0, 0] etc.
return as_vector(
[ten[0, 0], ten[1, 1], ten[2, 2], 2 * ten[1, 2], 2 * ten[0, 2], 2 * ten[0, 1]]
)
# rewrite a vector into a tensor using Voigt notation
def voigt3stress(vec):
# FEniCS does not know anything about Voigt notation,
# so one need to rewrite the vector by hand into a tensor.
return as_tensor(
[[vec[0], vec[5], vec[4]], [vec[5], vec[1], vec[3]], [vec[4], vec[3], vec[2]]]
)
# first define the function for the strain tensor in fenics notation
def B(u):
# note that it would be shorter to use sym(grad(u)) but the way used now
# represents the formula
return 1.0 / 2.0 * (grad(u) + (grad(u).T))
# define the electric field vector
def E_field_val_vector(Ei):
return as_vector([Ei[0], Ei[1], Ei[2]])
# define the electric field in relation to potential
def elect_field_E(phi):
return -grad(phi)
# sigma for coupled linear elasicity and electrostatics
def sigma(u, phi):
return voigt3stress(
dot(C, strain3voigt(B(u))) + dot(E_t_piezo , E_field_val_vector(elect_field_E(phi)))
)
# the electric displacements vector
def disp_D(Di):
return as_vector([Di[0], Di[1], Di[2]])
# definition of the different components of my electric displacements equation (D=e^s:Bu+eps^S.E)
# elect_disp_D for coupled linear elasicity and electrostatics
def elect_disp_D(u, phi):
elect_disp = dot(E_piezo ,strain3voigt(B(u))) - dot(Eps_s , elect_field_E(phi))
return disp_D(elect_disp)
# define the potential
dt = 0.01
t = np.arange( -0.00098462, 20.0, dt)
# Amplitude of the sine wave is sine of a variable like time
potential = np.sin(3 * np.pi * (t - (20.0 / 2)))
phi = Expression("t", degree=0, t=potential[0])
# --------------------
# Boundary conditions
# --------------------
top_boundary = TopBoundary()
bottom_boundary = BottomBoundary()
# Create the boundary condition for displacement
boundary = []
boundary.append(DirichletBC(M.sub(2), 0.0, bottom_boundary))
boundary.append(DirichletBC(M.sub(2), phi, top_boundary))
for i in range(len(t)):
phi.t = t[i]
print(assemble(phi * dx(domain=mesh)))
# As the stress is defined over the outer surface we need to create a
# integral over that surface
boundaries = MeshFunction("size_t", mesh, mesh.topology().dim() - 1)
boundaries.set_all(0)
top_boundary.mark(boundaries, 1)
bottom_boundary.mark(boundaries, 2)
dx = Measure("dx", domain=mesh)
ds = Measure("ds", subdomain_data=boundaries)
mf = MeshFunction("size_t", mesh, mesh.topology().dim() - 1)
mf.set_all(0)
top_boundary.mark(mf, 1)
bottom_boundary.mark(mf, 2)
# the initial values
zero1d = Expression("0.0", degree=1)
zero3d = Expression(("0.0", "0.0", "0.0"), degree=1)
u0 = interpolate(zero3d, M.sub(0).collapse())
z0 = interpolate(zero3d, M.sub(1).collapse())
phi0 = interpolate(zero1d, M.sub(2).collapse())
# --------------------
# Function spaces
# --------------------
# Defining the "Trial" functions
u1, z1, phi1 = TrialFunctions(M)
# Defining the "Test" functions
v, y, w = TestFunctions(M)
# --------------------
# Weak form
# --------------------
tmps = Function(M)
a = (
rho_Piezo * inner(z1, v) * dx
+ theta * dt * inner(sigma(u1, phi1), B(v)) * dx
+ theta * dt * alpha * rho_Piezo * inner(z1, v) * dx
+ theta * dt * beta * inner(dot(C, strain3voigt(B(z1))), strain3voigt(B(v))) * dx
+ inner(elect_disp_D(u1, phi1), grad(w)) * dx
+ inner(u1, y) * dx
- theta * dt * (inner(z1, y)) * dx
)
l = (
-rho_Piezo * inner(z0, v) * dx
+ theta * dt * inner(sigma(u0, phi0), B(v)) * dx
+ theta * dt * alpha * rho_Piezo * inner(z0, v) * dx
+ theta * dt * beta * inner(dot(C, strain3voigt(B(z0))), strain3voigt(B(v))) * dx
- inner(u0, y) * dx
- theta * dt * (inner(z0, y)) * dx
)
# assemble only A and L
A = assemble(a)
L = assemble(-l)
# apply A and L
for bc in boundary:
bc.apply(A, L)
# solve the weak equation
solve(A, tmps.vector(), L)
u_result, z_result, phi_result = tmps.split()
FunctionAssigner(
[M.sub(0).collapse(), M.sub(1).collapse(), M.sub(2).collapse()],
tmps.function_space(),
)
assign(tmps.sub(0), u0)
assign(tmps.sub(1), z0)
assign(tmps.sub(2), phi0)
vtkfile = File("phi_result.pvd")
vtkfile << phi_result
the result I’d like to have.