Hi all!
I’m working on a coupled advection-diffusion problem in dolfinx v0.9.0, and I’ve come across a behaviour I don’t fully understand, hoping someone might have seen something similar or has some ideas as to what’s going on.
I start by solving the steady-state incompressible Navier–Stokes equations in a lid-driven cavity:
\begin{aligned}
\left( \mathbf{u} \cdot \nabla \mathbf{u} \right) - \mu \nabla^2 \mathbf{u} + \nabla p &= 0 \\\\
\nabla \cdot \mathbf{u} &= 0
\end{aligned}
with no-slip on all walls and a fixed velocity on the top. Resulting in the following:
I use this velocity field in a transient advection-diffusion simulation:
\frac{\partial c}{\partial t} + \mathbf{u} \cdot \nabla c - D \nabla^2 c = S
The diffusing species has a source that is active for a short time and then turned off. I apply a Dirichlet boundary condition c = 0 on the top wall, and no-flux (Neumann = 0) on all other sides.
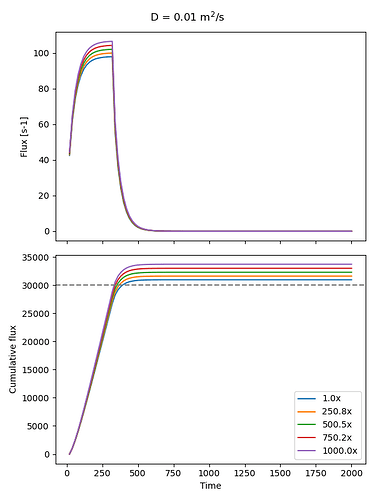
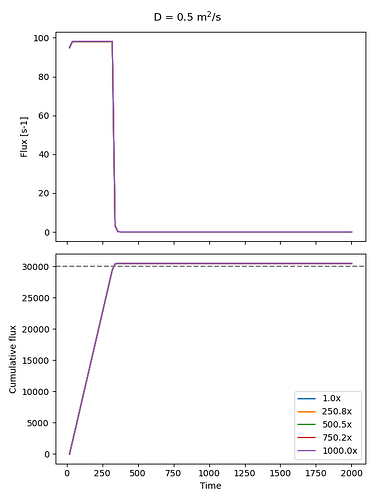
What I expected: the larger the velocity term, the faster the diffusing species would be flushed out through the top. But what I’m seeing instead is that the rate at which the diffusing species leaves the system doesn’t change much with velocity. Strangely, the total cumulative flux at the top boundary actually increases with higher velocity, even though the source adds the same amount each time. So, effectively, the system is seeming leaking mass that doesn’t exist.
Not sure if this could be something to do with time-stepping, the way I’m imposing boundary conditions, integrated the advection term in the diffusion problem, or something deeper like stabilisation issues or numerical diffusion, or probably more likely, something fundamental I’ve misunderstood in this problem. Any thoughts or similar experiences would be great to hear.
import numpy as np
from mpi4py import MPI
from petsc4py import PETSc
import ufl
from dolfinx import mesh, fem, io
from dolfinx.mesh import CellType, create_unit_square, meshtags
from dolfinx.fem.petsc import NonlinearProblem
from dolfinx.nls.petsc import NewtonSolver
from dolfinx.log import set_log_level, LogLevel
import basix
import adios4dolfinx
def top_surface(x):
return np.isclose(x[1], 1.0)
def lid_driven_cavity():
domain = create_unit_square(MPI.COMM_WORLD, 50, 50, CellType.triangle)
# Define Taylor-Hood element (P2-P1)
element_u = basix.ufl.element(
"Lagrange", domain.basix_cell(), 2, shape=(domain.geometry.dim,)
)
element_p = basix.ufl.element("Lagrange", domain.basix_cell(), 1)
mixed_ele = basix.ufl.mixed_element([element_u, element_p])
# define function space and colla
W = fem.functionspace(domain, mixed_ele)
V_collapsed, _ = W.sub(0).collapse()
# Functions and test functions
up = fem.Function(W)
v_q = ufl.TestFunctions(W)
v, q = v_q
u, p = ufl.split(up)
# Viscosity
nu = 1e-03
# top wall velocity bc
lid_u = fem.Function(V_collapsed)
lid_u.interpolate(
lambda x: np.array([1e-4 * np.ones(x.shape[1]), np.zeros(x.shape[1])])
)
facets_lid = mesh.locate_entities_boundary(
domain, domain.topology.dim - 1, top_surface
)
dofs_lid = fem.locate_dofs_topological((W.sub(0), V_collapsed), 1, facets_lid)
bc_lid = fem.dirichletbc(lid_u, dofs_lid, W.sub(0))
# No-slip walls bcs
def walls(x):
return np.isclose(x[0], 0.0) | np.isclose(x[0], 1.0) | np.isclose(x[1], 0.0)
wall_facets = mesh.locate_entities_boundary(domain, domain.topology.dim - 1, walls)
wall_dofs = fem.locate_dofs_topological((W.sub(0), V_collapsed), 1, wall_facets)
u_noslip = fem.Function(V_collapsed)
u_noslip.x.array[:] = 0.0
bc_walls = fem.dirichletbc(u_noslip, wall_dofs, W.sub(0))
bcs = [bc_lid, bc_walls]
dx = ufl.Measure("dx", domain=domain)
# Define variational problem (steady Navier-Stokes)
F = (
nu * ufl.inner(ufl.grad(u), ufl.grad(v)) * dx
+ ufl.inner(ufl.grad(u) * u, v) * dx
- p * ufl.div(v) * dx
- q * ufl.div(u) * dx
)
J = ufl.derivative(F, up)
set_log_level(LogLevel.INFO)
# Create nonlinear problem and solver
problem = NonlinearProblem(F, up, bcs, J)
solver = NewtonSolver(MPI.COMM_WORLD, problem)
solver.convergence_criterion = "incremental"
solver.atol = 1e-10
solver.rtol = 1e-8
solver.max_it = 50
solver.report = True
ksp = solver.krylov_solver
opts = PETSc.Options()
option_prefix = ksp.getOptionsPrefix()
opts[f"{option_prefix}ksp_type"] = "gmres"
opts[f"{option_prefix}pc_type"] = "gamg"
ksp.setFromOptions()
# Solve
n, converged = solver.solve(up)
print(f"Converged: {converged} in {n} Newton iterations")
# Extract solutions
uh, ph = up.sub(0).collapse(), up.sub(1).collapse()
uh.name = "velocity"
ph.name = "pressure"
# Save solution to file
writer = io.VTXWriter(MPI.COMM_WORLD, "lid_driven_cavity.bp", uh, "BP5")
writer.write(t=0)
# write checkpoints file
adios4dolfinx.write_mesh("lid_driven_cavity_cp.bp", mesh=domain)
adios4dolfinx.write_function("lid_driven_cavity_cp.bp", uh, time=0.0)
def advection_diffusion(domain, velocity_field):
# Define Lagrange element (P1)
element = basix.ufl.element("P", domain.basix_cell(), 1)
V = fem.functionspace(domain, element)
# Functions and test functions
u = fem.Function(V)
u_n = fem.Function(V)
v = ufl.TestFunction(V)
# Diffusion coefficient
D = 1e-3
facets_lid = mesh.locate_entities_boundary(
domain, domain.topology.dim - 1, top_surface
)
dofs_lid = fem.locate_dofs_topological(V, 1, facets_lid)
bc_top = fem.dirichletbc(fem.Constant(domain, PETSc.ScalarType(0)), dofs_lid, V)
# source term only active for first 300 seconds then zero
source_value = lambda t: 100 if t <= 300 else 0
source = fem.Constant(domain, PETSc.ScalarType(source_value(t=0)))
dt = fem.Constant(domain, PETSc.ScalarType(20))
vdim = domain.topology.dim
num_cells = domain.topology.index_map(vdim).size_local
mesh_cell_indices = np.arange(num_cells, dtype=np.int32)
tags_volumes = np.full(num_cells, 1, dtype=np.int32)
vmt = meshtags(domain, vdim, mesh_cell_indices, tags_volumes)
dx = ufl.Measure("dx", domain=domain, subdomain_data=vmt)
bcs = [bc_top]
# Define variational problem (steady diffusion)
F = D * ufl.inner(ufl.grad(u), ufl.grad(v)) * dx
F += ((u - u_n) / dt) * v * dx
F += ufl.inner(ufl.dot(ufl.grad(u), velocity_field), v) * dx
F -= source * v * dx
problem = fem.petsc.NonlinearProblem(
F,
u,
bcs,
)
solver = NewtonSolver(MPI.COMM_WORLD, problem)
solver.convergence_criterion = "incremental"
solver.atol = 1e-12
solver.rtol = 1e-12
solver.max_it = 30
ksp = solver.krylov_solver
ksp.setType("preonly")
ksp.getPC().setType("lu")
ksp.getPC().setFactorSolverType("mumps")
ksp.setErrorIfNotConverged(True)
final_time = 2000
t = fem.Constant(domain, PETSc.ScalarType(0))
n = ufl.FacetNormal(domain)
ds = ufl.Measure("ds", domain=domain)
times, top_flux = [], []
while t.value < final_time:
source.value = source_value(t=t.value)
t.value += dt.value
solver.solve(u)
u_n.x.array[:] = u.x.array[:]
top_flux_value = fem.assemble_scalar(
fem.form(-D * ufl.dot(ufl.grad(u), n) * ds)
)
advective_flux = fem.assemble_scalar(
fem.form(ufl.inner(velocity_field, n) * u * ds)
)
top_flux.append(top_flux_value + advective_flux)
times.append(float(t.value))
return times, top_flux
def read_velocity(filename):
# Read the velocity field from the lid-driven cavity simulation
domain = adios4dolfinx.read_mesh(filename, MPI.COMM_WORLD)
P2 = basix.ufl.element(
"Lagrange", domain.basix_cell(), 2, shape=(domain.geometry.dim,)
)
V = fem.functionspace(domain, P2)
u_ldc = fem.Function(V)
u_ldc.name = "velocity"
adios4dolfinx.read_function(filename, u_ldc, time=0.0)
return u_ldc
if __name__ == "__main__":
force_cfd = False
if force_cfd:
lid_driven_cavity()
import matplotlib.pyplot as plt
from scipy.integrate import cumulative_trapezoid
# Run the advection-diffusion simulation
fig, axs = plt.subplots(2, 1, figsize=(6, 8), sharex=True)
for scaling_factor in np.linspace(1, 1000, num=5):
print(f"Scaling factor: {scaling_factor:.1f}")
u_ldc = read_velocity("lid_driven_cavity_cp.bp")
u_ldc.x.array[:] *= scaling_factor
t, top_flux = advection_diffusion(
domain=u_ldc.function_space.mesh, velocity_field=u_ldc
)
axs[0].plot(t, top_flux, label="Top Flux")
integral_flux = cumulative_trapezoid(top_flux, x=t, initial=0)
axs[1].plot(t, integral_flux, label=f"{scaling_factor:.1f}x")
axs[0].set_ylabel("Flux [s-1]")
axs[1].set_ylabel("Cumulative flux")
axs[1].set_xlabel("Time")
plt.tight_layout()
plt.legend()
plt.show()