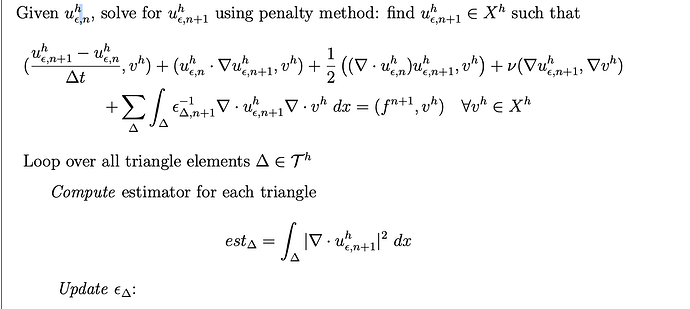Hello,
Could you please give some suggestions on how to calculate the L2 norm over each cell?
I am having a coeffient in the weak form that for cell-wise constant. I assume the coeffiicent is DG0, then I map it to P2, since that is my solution space.
Addition, I need to update my coefficient by calcuating some quantities on each cell.
If you have a way or thoughts, please let me know!
Thank you so much for help!
I did this, the norm is 0 on the cell:
dx_= ufl.Measure("dx", msh, subdomain_data=cell_tags)
for cell in range(msh.topology.index_map(msh.topology.dim).size_local):
print(cell)
#dofs_cell = V.dofmap.cell_dofs(cell)
error = np.sqrt(msh.comm.allreduce(assemble_scalar(fem.form(inner(u_exact_fem, u_exact_fem)*dx_(cell))), op=MPI.SUM))
print("L2 norm")
print(error)
error = np.sqrt(msh.comm.allreduce(assemble_scalar(fem.form(inner(u_exact_fem, u_exact_fem)*dx)), op=MPI.SUM))
print("total", error)
Please quote your code properly.
With
dx_= ufl.Measure("dx", msh, subdomain_data=cell_tags)
you are saying that the cell markers to be used when defining the measure dx are those present in cell_tags. Unless you have a different marker for every cell, dx_(cell) will either give you an integral on more than one cell (if the numeric value associate do the current index cell is present in cell_tags), or an integral over an empty domain (otherwise). In the former case you’d get a wrong result, in the latter you’d get zero.
To get what you want, define a v_DG0 as a test function on a DG 0 space, and assemble the form
inner(u_exact_fem, u_exact_fem) * v_DG0 * ufl.dx
using assemble_vector.
The result will be a vector which has as many entries as the number of cells. If I remember correctly, the order of the DOFs of the DG0 space is the same as the order of the cells (i.e., the first entry of the vector will be the L2 norm in the first cell), but I can’t test this assumption without a MWE.
Thank you so much for your help @francesco-ballarin. My bad, I should have uploaded some mini-code.
I am working on a time-dependent 2D Navier Stokes equation with an adaptive scheme, in which the penalty parameter varies for each cell, or we call it an element over the domain. My approach is to define a DG0 array that stores the penalty parameter for each cell. Then I solve the matrix, update my solution, and calculate some quantity on each cell as a criterion to update my penalty parameter for the next time step. Repeat this.
Do you think it will be reseaonale, I don’t know how to assemble the matrix while some coefficient is defined for each cell. I provide my code, which runs with no error if that helps.
Thank you!
from mpi4py import MPI
from petsc4py import PETSc
import dolfinx
from dolfinx import fem, mesh, io
from dolfinx.fem import Constant
from dolfinx.fem.assemble import assemble_matrix, create_vector, assemble_vector, apply_lifting, set_bc, assemble_scalar
import ufl
from ufl import div, dot, dx, inner, lhs, nabla_grad, rhs, grad
class Velocity:
def __init__(self):
self.t = 0.0
def eval(self, x):
# Added some spatial variation here.
return (np.pi * np.sin(self.t) * np.sin(2 * np.pi * x[1]) * (np.sin(np.pi * x[0])) ** 2,
-np.pi * np.sin(self.t) * np.sin(2 * np.pi * x[0]) * (np.sin(np.pi * x[1])) ** 2)
class Pressure:
def __init__(self):
self.t = 0.0
def eval(self, x):
return np.sin(self.t) *np.cos(np.pi * x[0]) * np.sin(np.pi * x[1])
class Source:
def __init__(self):
self.t=0.0
def eval(self, x):
return (np.pi*(4*np.pi**2*np.sin(self.t)**2*np.sin(np.pi*x[0])**3*np.sin(np.pi*x[1])*np.cos(np.pi*x[0]) +16*np.pi**2*np.sin(self.t)*np.sin(np.pi*x[0])**2*np.cos(np.pi*x[1]) - np.sin(self.t)*np.sin(np.pi*x[0]) - 4*np.pi**2*np.sin(self.t)*np.cos(np.pi*x[1]) + 2*np.sin(np.pi*x[0])**2*np.cos(self.t)*np.cos(np.pi*x[1]))*np.sin(np.pi*x[1]),
np.pi*(4*np.pi**2*np.sin(self.t)**2*np.sin(np.pi*x[0])**2*np.sin(np.pi*x[1])**3*np.cos(np.pi*x[1]) - 16*np.pi**2*np.sin(self.t)*np.sin(np.pi*x[0])*np.sin(np.pi*x[1])**2*np.cos(np.pi*x[0]) + 4*np.pi**2*np.sin(self.t)*np.sin(np.pi*x[0])*np.cos(np.pi*x[0]) + np.sin(self.t)*np.cos(np.pi*x[0])*np.cos(np.pi*x[1]) - 2*np.sin(np.pi*x[0])*np.sin(np.pi*x[1])**2*np.cos(self.t)*np.cos(np.pi*x[0])))
#exact solution of the test problem
u_exact = Velocity()
p_exact = Pressure()
f = Source()
# define mesh
nx = 2
ny = 2
msh = mesh.create_rectangle(MPI.COMM_WORLD, [np.array([-1, -1]), np.array([1, 1])], [nx, ny], dolfinx.cpp.mesh.CellType.triangle)
cell=msh.ufl_cell()
tdim = msh.topology.dim
num_cells = msh.topology.index_map(tdim).size_local
h = dolfinx.cpp.mesh.h(msh, tdim, range(num_cells)) #h is the largest edge
print("edge length", h)
DG0 = dolfinx.fem.FunctionSpace(msh, ("DG", 0))
v_DG0 = ufl.TestFunction(DG0)
# define function space
P2 = ufl.VectorElement("CG", cell, 2)
V = fem.FunctionSpace(msh, P2)
DG0_ufl = ufl.FiniteElement("DG", cell, 0)
V0 = fem.FunctionSpace(msh, DG0_ufl)
piecewise_coef =fem.Function(V0)
piecewise_coef.name = "piecewise_coef"
for i in range(len(piecewise_coef.x.array[:])):
piecewise_coef.x.array[i] = (i+1)*1e-3
"""useful expressions"""
def b(u, v, w): # Skew-symmetry nonlinear term
return .5 * (inner(dot(u, nabla_grad(v)), w) - inner(dot(u, nabla_grad(w)), v))
def a(u, v): # Viscous term (grad(u),grad(v))
return inner(nabla_grad(u), nabla_grad(v))
# define the velocity trial and test functions
u = ufl.TrialFunction(V)
v = ufl.TestFunction(V)
# define boundary conditions
from petsc4py.PETSc import ScalarType
uD = fem.Constant(msh, ScalarType((0.0,0.0)))
# Create facet to cell connectivity required to determine boundary facets
tdim = msh.topology.dim
fdim = tdim - 1
msh.topology.create_connectivity(fdim, tdim)
boundary_facets = mesh.exterior_facet_indices(msh.topology)
boundary_dofs = fem.locate_dofs_topological(V, fdim, boundary_facets)
bcu = fem.dirichletbc(uD, boundary_dofs,V)
bcs = [bcu]
# define the solution fields involved
u_exact_fem = fem.Function(V)
u_exact_fem.name = "u_exact_fem"
u_n = fem.Function(V)
u_n.name = "u_n"
u_next = fem.Function(V)
u_next.name = "u_next"
f_fem = fem.Function(V)
f_fem.name = "f_fem"
time_step = 0.1
nu = 1
t =0
t += time_step
#u_n
t += time_step
u_exact.t = t
u_n=fem.Function(V)
u_n.name = "u_n"
u_n.interpolate(u_exact.eval)
u_n.x.scatter_forward()
"""" algorithm """
F3 = 1.0 / time_step * inner(u, v) * dx
F3 += b(u_n, u, v) * dx
F3 += 1/piecewise_coef * div(u) * div(v) * dx #here
F3 += nu * a(u, v) * dx
F3 -= 1.0 / time_step * inner(u_n, v) * dx + inner(f_fem, v) * dx
a3 = fem.form(lhs(F3))
L3 = fem.form(rhs(F3))
A3 = fem.petsc.create_matrix(a3)
b3= fem.petsc.create_vector(L3)
#Direct Solver for NSE before turning on k equation
ksp3 = PETSc.KSP().create(msh.comm)
ksp3.setOperators(A3)
ksp3.setType("preonly")
pc3 = ksp3.getPC()
pc3.setType("lu")
pc3.setFactorSolverType("mumps")
pc3.setFactorSetUpSolverType()
# update time
t += time_step
f.t = t
u_exact.t = t
f_fem.interpolate(f.eval)
u_exact_fem.interpolate(u_exact.eval)
A3.zeroEntries()
fem.petsc.assemble_matrix(A3, a3, bcs=bcs)
A3.assemble()
with b3.localForm() as loc:
loc.set(0)
fem.petsc.assemble_vector(b3, L3)
fem.petsc.apply_lifting(b3, [a3], [bcs])
b3.ghostUpdate(addv=PETSc.InsertMode.ADD_VALUES, mode=PETSc.ScatterMode.REVERSE)
fem.petsc.set_bc(b3, bcs)
ksp3.solve(b3, u_next.vector)
u_next.x.scatter_forward()
divu_form = dolfinx.fem.form(inner(div(u_next), div(u_next))*v_DG0*ufl.dx)
divu_norm_element =dolfinx.fem.assemble_vector(divu_form )
print("francesco")
print(divu_norm_element.array)@francesco-ballarin one thing, i try to put the DG0 coefficient to the weak form and assemble the matrix, it returns me no error. I wander if Fenicsx would know that I meant the coefficient is constant on each cell, when they assemble the matrix.
Will FEniCSx the finite element method take into account the piecewise constant nature of DG0 functions over each cell during the assembly of the system matrix.
Thank you!
Can you format your code properly with “```”, and report the error? It should have been possible to store the result in a the vector associated to a dolfinx.fem.Function, and then use it in the ufl form.
Even better, please try to simplify your code. There are a lot of steps in there, and it would helpful if you could boil it down to the bare minimum.
Thank you so much!! I just formatted my code and I tried to get rid of the unnecessary part and simplify my problem.
My code can run successfully.
I wonder how to implement my piecewise constant coefficient for each cell and solve the system. I used to have a constant for the divergence term, but now I am adapting it. I have the coefficient stored as DG0, can I have DG0 coefficient (div (u), div(v)) dx, where my u is P2. I hope the algorithm picture helps.
I found this, Defining subdomains for different materials — FEniCSx tutorial, for subdomains, they use DG0 to define the coefficient. Do you think I can similar thing but my coefficients vary for each cell?
Thank you!
Yes, that should be the right idea.
