Dear community,
how to test convergence of the spatial discretization of the transient heat equation with Legacy FEniCS is well documented, see here and open the downloaded .html file.
In summary, you determine the averaged error E between an assumed analytical solution u_\mathrm{e} and the numerically calculated solution u for an increasing amount of elements n_\mathrm{s}.
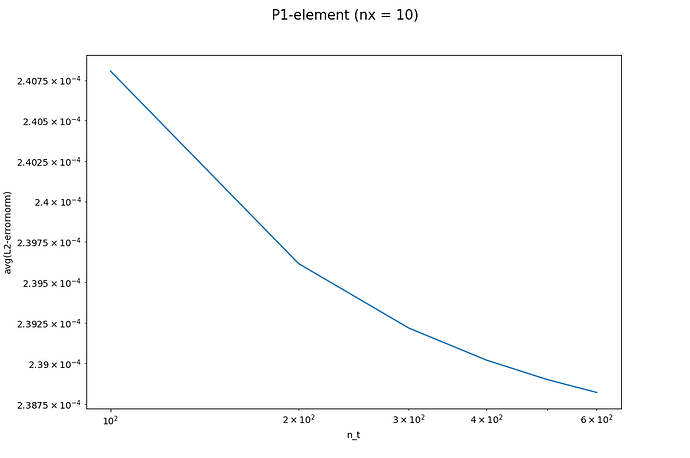
I used the same procedure, with the only difference, that I increased the amount of time steps n_\mathrm{t}, to test the convergence of the temporal discretization by using the forward-Euler method (CFL-conditions are satisfied), but didn’t get a linear correlation between time steps and L2-error for double logarithmic scales, see figure below.
It also yields convergence rates r far smaller than 2 (elements with degree = 1 were used). Convergence rates r of two neighbouring amount of time steps i and i-1 were calculated by
| i | 1 | 2 | 3 | 4 | 5 | 6 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| time steps n_\mathrm{t} | 100 | 200 | 300 | 400 | 500 | 600 | |||||
| convergence rate r | 0.007151622055142903 | 0.00408879703330978 | 0.0028850131814337193 | 0.0022331434928824093 | 0.0018228565668401908 |
That’s why the following questions come to mind…
1. Is this procedure adequate to test convergence of the temporal discretization by using the forward-Euler method?
2. If so, do the results prove a successful temporal discretization?
If you´re interested in the MWCE of an 1-d transient heat equation with Dirichlet boundary conditions, open the spoiler and run the code with FEniCS Legacy.
MWCE
"""
FEniCS tutorial demo program: 1d-Heat equation with Dirichlet conditions.
Test problem is chosen to give an exact solution at all nodes of the mesh.
Temporal discretization scheme: explicit forward-EULER
u' = D*Laplace(u) + f in the unit line
u_e = u_D = alpha - t * sin(x) / T
u = u_D on the boundary
u = u_D(t=0) at t = 0
u' = - sin(x) / T
Laplace(u) = t * sin(x) / T
f = - sin(x) / T - D * t * sin(x) / T
"""
import matplotlib.pyplot as plt
import numpy as np
from fenics import *
set_log_level(30)
def solver(D, dt, num_steps, degree, mesh, V, alpha):
""" Solves variational problem and calc L2-error between solution u and exact analytical solution u_e"""
# CFL check because of explicit forward EULER
element_size = mesh.hmin()
CFL = D * dt / element_size
if CFL > 1.0:
sys.exit("CFL-conditions not satisfied (CFL> 1)!")
# Define DIRICHLET boundary condition
u_D = Expression('alpha - t*sin(x[0])/T', alpha=alpha, t=0, T=T, degree=degree)
def boundary(x, on_boundary):
return on_boundary
bc = DirichletBC(V, u_D, boundary)
# Define exact analytical solution
u_e = Expression('alpha - t*sin(x[0])/T', alpha=alpha, t=0, T=T, degree=degree+1+3)
# Initialize list to save L2 errornorm between u_e and u
L2_err_list = []
# Define initial value
u_n = interpolate(u_D, V)
# Define variational problem
u = TrialFunction(V)
v = TestFunction(V)
f_n = Expression('- sin(x[0]) / T - D * t * sin(x[0]) / T', D=D, t=0, T=T, degree=degree)
# Weak form
F = u * v * dx + dt * D * dot(grad(u_n), grad(v)) * dx - (u_n + dt * f_n) * v * dx
a, L = lhs(F), rhs(F)
# Time-stepping
u = Function(V)
t = 0
for n in range(num_steps):
# Update to current time
t += dt
u_D.t = t
u_e.t = t
# Compute solution u
solve(a == L, u, bc)
# Compute L2-error and add to list
L2_err_list += [errornorm(u_e, u, 'L2', degree_rise=3)]
# Update for next time step
u_n.assign(u)
f_n.t = t
# Calc average L2-error
L2_err_avg = 1/len(L2_err_list) * sum(L2_err_list)
return L2_err_avg
def run_spatial_convergence_analysis(nx, num_steps, D, degree, alpha):
# Initialize list to save average L2-errornorms
L2_err_avg_list = []
# Iterate through nx
for i in range(len(nx)):
# Create mesh and define function space
mesh = IntervalMesh(nx[i], 0, 1)
V = FunctionSpace(mesh, 'P', degree)
# Calc time step dt
dt = T / num_steps[0]
# Calc average L2-errornorm between u_e and u by running solver
L2_err_avg = solver(D, dt, num_steps[0], degree, mesh, V, alpha)
# Add average L2-errornorm to list
L2_err_avg_list += [L2_err_avg]
return L2_err_avg_list
def run_temporal_convergence_analysis(nx, num_steps, D, degree, alpha):
# Initialize list to save average L2-errornorms
L2_err_avg_list = []
# Iterate through num steps
for i in range(len(num_steps)):
# Create mesh and define function space
mesh = IntervalMesh(nx[0], 0, 1)
V = FunctionSpace(mesh, 'P', degree)
# Calc time step dt
dt = T / num_steps[i]
# Calc average L2-errornorm between u_e and u by running solver
L2_err_avg = solver(D, dt, num_steps[i], degree, mesh, V, alpha)
# Add average L2-errornorm to list
L2_err_avg_list += [L2_err_avg]
return L2_err_avg_list
def compute__convergence_rate(L2_error_avg_list, nx, num_steps, time_or_space):
# Initialize h
h = []
# Calc h
if time_or_space == 'time':
for i in range(len(num_steps)):
h += [1 / num_steps[i]]
elif time_or_space == 'space':
for i in range(len(nx)):
h += [1 / nx[i]]
# Initialize rate
rate = [[] for _ in range(len(h) - 1)]
# Calc rate
for m in range(len(h) - 1):
rate[m] += [np.log(L2_error_avg_list[m + 1] / L2_error_avg_list[m]) / np.log(h[m + 1] / h[m])]
# Print rate
if time_or_space == 'time':
print('rate(temporal)) = ', rate)
elif time_or_space == 'space':
print('rate(spatial)) = ', rate)
def plot_result_of_convergence_analysis(nx, num_steps, L2_err_avg_list, degree, time_or_space):
fig, ax = plt.subplots()
plt.yscale("log")
plt.xscale("log")
ax.set_ylabel("avg(L2-errornorm)")
if time_or_space == 'time':
fig.suptitle(f'P{degree}-element (nx = {nx})', fontsize=15)
ax.set_xlabel('n_t')
ax.plot(num_steps, L2_err_avg_list)
elif time_or_space == 'space':
fig.suptitle(f'P{degree}-element (num steps = {num_steps})', fontsize=15)
ax.set_xlabel("n_x")
ax.plot(nx, L2_err_avg_list)
# Parameters
D = 0.005 # diffusion coefficient
T = 1.0 # final time
num_steps = [100,200,300,400,500,600] # number of time steps
nx = [10,20,30,40,50,60] # elements per mesh
degree = 1 # element degree
alpha = 1.0 # parameter for exact analytical solution
# Run convergence analysis
L2_err_avg_list_spatial = run_spatial_convergence_analysis (nx, num_steps, D, degree, alpha) # spatial
L2_err_avg_list_temporal = run_temporal_convergence_analysis(nx, num_steps, D, degree, alpha) # temporal
# Compute convergence rate
compute__convergence_rate(L2_err_avg_list_spatial , nx, num_steps, 'space') # spatial
compute__convergence_rate(L2_err_avg_list_temporal, nx, num_steps, 'time') # temporal
# Plot result of convergence analysis
plot_result_of_convergence_analysis(nx , num_steps[0], L2_err_avg_list_spatial , degree, 'space') # spatial
plot_result_of_convergence_analysis(nx[0], num_steps , L2_err_avg_list_temporal, degree, 'time') # temporal
plt.show()