Improve mapping data on a Function by coordinates

[Eduardo_Firvida]

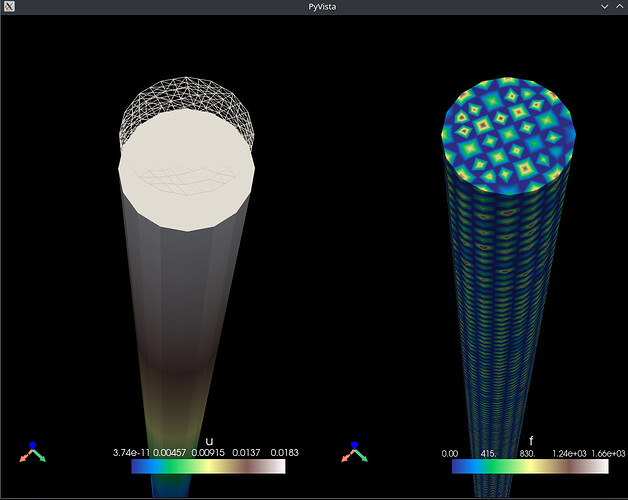
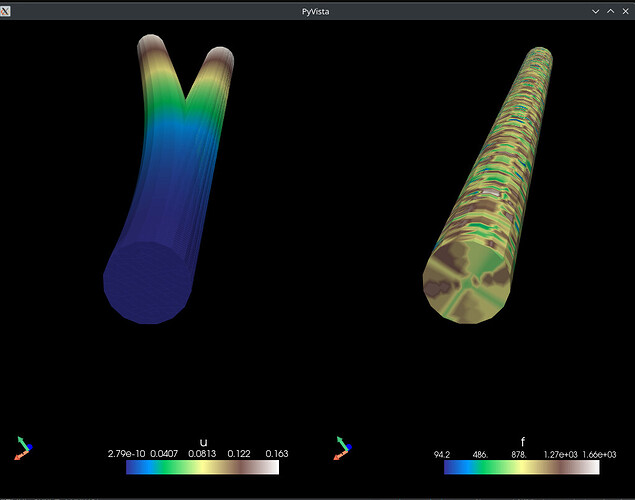
Hi everyone, I have a working code that I want to improve, I simplified a lot to create a MWE.

I’m triying to couple Fenics-X via preCICE by myself, because the current adapter can solve 3D linear elastic problems at the moment.

So, to work with preCICE, I have to provide the mesh node coordinates of the coupling interface, then it will interpolate de compute data from the coupled solver, to that nodes. And I need to apply that computed data to the fenicsx model.

So in my code:

1. I get the interface node coordinates directly from the gmsh model. but I want to get it from the mesh domain.
2. Then I have in return (this is simulated in the MWE) an array of loads, in the same order of the nodes I give.
3. I search the index of the nodes in the fenicsx mesh, by searching for the coords returned in step 1.
4. finally I create a load Function over the FunctioSpace and map the array of loads to the function space.

At this point the code works but have a lot of issues. First the performance issue that implies extracting and the remapping the coordinates, as described in point 1, and 3. The other big issue is that this approach don’t work with a second order elelemt and function space.

import os
from typing import NamedTuple

import gmsh
import numpy as np
import pyvista
import ufl
from dolfinx import fem, io, mesh, plot
from dolfinx.fem.petsc import LinearProblem
from mpi4py import MPI
from petsc4py import PETSc

comm = MPI.COMM_WORLD
CURRENT_FOLDER = os.path.dirname(__file__)


# -------------------#
# Problem properties #
# -------------------#
class Material(NamedTuple):
    name: str
    E: PETSc.ScalarType
    nu: PETSc.ScalarType
    rho: PETSc.ScalarType


material = Material("Aluminum 6061", 68.9e9, 0.33, 2700)

# beam size
height = 150  # m
diameter = 6.5  # m


# ------- #
# MESHING #
# ------- #
FIXED_TAG = 1000
LOAD_SURFACE_TAG = 3000
VOLUME_TAG = 4000
ELEMENTS_ORDER = 1


def gmsh_tower(h: float, d: float) -> gmsh.model:
    model_name = "Tower"
    gmsh.model.add(model_name)

    model = gmsh.model()
    model.setCurrent(model_name)

    # Recombine tetrahedra to hexahedra
    gmsh.option.setNumber("Mesh.RecombinationAlgorithm", 2)
    gmsh.option.setNumber("Mesh.RecombineAll", 2)
    gmsh.option.setNumber("Mesh.CharacteristicLengthFactor", 0.1)

    circle = model.occ.addDisk(0, 0, 0, d / 2, d / 2)
    model.occ.extrude([(2, circle)], 0, 0, h, numElements=[h], recombine=True)
    model.occ.synchronize()

    fixed_sf = model.addPhysicalGroup(2, [1], tag=FIXED_TAG)
    tip_sf = model.addPhysicalGroup(2, [2, 3], tag=LOAD_SURFACE_TAG)
    vol = model.addPhysicalGroup(3, [1], tag=VOLUME_TAG)

    model.setPhysicalName(2, fixed_sf, "FIXED SURFACE")
    model.setPhysicalName(2, tip_sf, "LOAD SURFACE")
    model.setPhysicalName(3, vol, "Mesh volume")

    model.mesh.setOrder(ELEMENTS_ORDER)
    model.mesh.generate(3)

    # get node coordinates of LOAD_SURFACE physical group
    boundaries = ((2, 2), (2, 3))
    interface_nodes = []
    for dim, tag in boundaries:
        tag = abs(tag)
        _, coords, _ = gmsh.model.mesh.getNodes(dim, tag, includeBoundary=True)
        interface_nodes.extend(coords)
    interface_nodes = np.array(interface_nodes).reshape((len(interface_nodes) // 3, 3))

    return model, interface_nodes


# Create model
gmsh.initialize()
gmsh.option.setNumber("General.Terminal", 0)
model, interface_nodes = gmsh_tower(height, diameter)
domain, cell_markers, facet_markers = io.gmshio.model_to_mesh(model, comm, rank=0)
dim = domain.geometry.dim
domain.topology.create_connectivity(dim - 1, dim)

# -------------- #
# Function Space #
# -------------- #
V = fem.functionspace(domain, ("Lagrange", ELEMENTS_ORDER, (dim,)))
u = fem.Function(V, name="Displacement")
f = fem.Function(V, name="Force")

E = fem.Constant(domain, float(material.E))
nu = fem.Constant(domain, float(material.nu))
rho = fem.Constant(domain, float(material.rho))


# ------------------------------------ #
# APPLY DISTRIBUTED LOADS ON BEAM FACE #
# ------------------------------------ #
def map_mesh_ids(global_matrix, loads_matrix):
    ids = []
    for c in loads_matrix:
        id = np.argwhere(np.all((global_matrix - c) == 0, axis=1)).item()
        ids.append(id)
    return ids


_loads_coords = interface_nodes
_domain_coords = domain.geometry.x
ids = map_mesh_ids(_domain_coords, _loads_coords)

# simulated preCICE response
external_loads = np.random.random(_loads_coords.shape) * 1000

_f = np.zeros(domain.geometry.x.shape)
_f[ids] = external_loads
f.x.array[:] = _f.flatten()
f.x.scatter_forward()


# --------------------#
# Boundary conditions #
# --------------------#
# Clamped
u_D = np.array([0, 0, 0], dtype=PETSc.ScalarType)
fixed_facets = facet_markers.find(FIXED_TAG)
fixed_surface_dofs = fem.locate_dofs_topological(V, 2, fixed_facets)
fixed_bc = fem.dirichletbc(u_D, fixed_surface_dofs, V)


# -------------------------#
# linear elastic equations #
# -------------------------#
load_facets = facet_markers.find(LOAD_SURFACE_TAG)
load_tags = mesh.meshtags(domain, dim - 1, np.sort(load_facets), 1)
ds = ufl.Measure("ds", domain=domain, subdomain_data=load_tags, subdomain_id=1)

lmbda = E * nu / (1 + nu) / (1 - 2 * nu)
mu = E / 2 / (1 + nu)


def epsilon(u):
    return ufl.sym(ufl.grad(u))


def sigma(u):
    return lmbda * ufl.nabla_div(u) * ufl.Identity(len(u)) + 2 * mu * epsilon(u)


du = ufl.TrialFunction(V)
u_ = ufl.TestFunction(V)
a = ufl.inner(sigma(du), epsilon(u_)) * ufl.dx
l = ufl.inner(f, u_) * ds(1)

bcs = [fixed_bc]
problem = LinearProblem(a, l, bcs=bcs, u=u, petsc_options={"ksp_type": "cg", "pc_type": "gamg"})

uh = problem.solve()


# ------------ #
# PLOT RESULTS #
# ------------ #

p = pyvista.Plotter(shape=(1, 2), theme=pyvista.themes.DarkTheme())
topology, cell_types, geometry = plot.vtk_mesh(V)
grid = pyvista.UnstructuredGrid(topology, cell_types, geometry)
grid["u"] = u.x.array.reshape((geometry.shape[0], 3))
grid["f"] = f.x.array.reshape((geometry.shape[0], 3))

p.subplot(0, 0)
grid.set_active_scalars("u")
p.add_mesh(grid.copy(), style="wireframe", cmap="terrain")
warped = grid.warp_by_vector("u", factor=100)
p.add_mesh(warped, show_edges=False, cmap="terrain")
p.add_axes(line_width=5, cone_radius=0.6, shaft_length=0.7, tip_length=0.3)

p.subplot(0, 1)
grid.set_active_scalars("f")
p.add_mesh(grid.copy(), show_edges=False, cmap="terrain")
p.add_axes(line_width=5, cone_radius=0.6, shaft_length=0.7, tip_length=0.3)

p.link_views()
p.show()

Result:

[Eduardo_Firvida]

I-m trygin this other approach which I thik I get rid of the first issue of mappgin the nodes with gmsh nodes. So now I-m using dof coordinates instead of nodes.

load_facets = facet_markers.find(LOAD_SURFACE_TAG)
load_tags = mesh.meshtags(domain, dim - 1, np.sort(load_facets), 1)
num_facets_owned_by_proc = domain.topology.index_map(fdim).size_local

geometry_entities = cpp.mesh.entities_to_geometry(domain._cpp_object, fdim, load_facets, False)

interface_dof_coords = []
for e in  geometry_entities:
    interface_dof_coords.extend(domain.geometry.x[e])
interface_dof_coords = np.array(interface_dof_coords)

# simulated preCICE response
external_loads = np.random.random(interface_dof_coords.shape) * 1000

Then I use a KDtree to proyect the external_loads data from the interface_dof_coords to the Function dofs. I tried some interpolations from scipy package, but this approach give the best results, until now. I think that I need to use the Function.interpolate method here, but I don[t know how to do it.

# create a dof index map by searching for closest coords from
# interface_dof_coords to vector spaces dofs
vector_space_coords = V.tabulate_dof_coordinates()
KDTree = spatial.KDTree(vector_space_coords)
dof_map = [KDTree.query(c)[1] for c in interface_dof_coords]

_f = np.zeros(vector_space_coords.shape)
_f[dof_map] = external_loads
f.x.array[:] = _f.flatten()
f.x.scatter_forward()

For second order mesh, and FunctionSpace, at least this approach is not exploding, but give very extrange results, so I’m sure that I’m misunderstanding something here

And example of a interpolations with scipy…

from scipy.interpolate import NearestNDInterpolator 
interpolator = NearestNDInterpolator(interface_coords, external_loads)
_f = interpolator(vector_space_coords)

The problem with this approach is that it put loads on the clamped boundary, which is wrong.

[dokken]

Note that you can use mesh.geometry.input_global_indices together with dolinx.mesh.entities_to_geometry to get the original node index in your Gmsh file.
https://docs.fenicsproject.org/dolfinx/v0.8.0/python/generated/dolfinx.cpp.mesh.html#dolfinx.cpp.mesh.Geometry_float32.input_global_indices

What is the difference between compute_incident_entities and entities_to_geometry?

entities to geometry computes the geometry (node indices) of an entity of any dimension (vertex, Edge, facet, cell). The nodes are listed per entity. Compute incident entities takes in a list of entities, and returns a single list of all entities of dimension d1 connected to these. In the case of a linear geometry, all nodes = vertices, and the connectivities might be the same for your call (not always guaranteed).

This is assuming you can extract the index from Gmsh in step 1.

[Eduardo_Firvida]

Dear @dokken thanks for your answer, that’s what I think I did in the first part of my second post. What I really need here are coordinates on the interface surface that I can use as reference points to apply the computational data given by the preCICE interface coupling. So Initialize the preCICE participat with that list of coordinates., and the library interpolate over that coordinates the data from the other solver. then I have in the Fenicsx part cords and data for each coord in the same order.

So I think that doesn’t matter if that coordinates are nodes or dogs, as long as they are consistents.

The problem now is as I understand on a 1 degree function space, dogs and nodes are the same, if I’m not wrong. Bot in and function space os degree 2, is not so simple. That’s were the things go crazy for me trying to map the external data over the Function where the coordinates that I have don’t match with the coordinates of the function space.

I’m going to try now with real data from the other participant to see what’s happen because random data are difficult to evaluate

[dokken]

@Eduardo_Firvida

Dear @dokken thanks for your answer, that’s what I think I did in the first part of my second post.

My point is that you never need to do a point search, as entities_to_geometry + input global indices gives you the node index in the gmsh mesh.

Also note that entities_to_geometry was recently extended to handle higher order geometries:

Orient mesh entities consistently and generalise `entities_to_geometry`

[Eduardo_Firvida]

Hi @dokken I think I found a better solution that may work ndependent of the mesher, and is a vector space degree friendly.

import dolfinx as dfx

def interpolation_points_in_vector_space(V, tags):
    fs_coords = V.tabulate_dof_coordinates()
    fdim = V.mesh.geometry.dim - 1
    boundary_dofs = dfx.fem.locate_dofs_topological(V, fdim, tags)
    boundary_coords = fs_coords[boundary_dofs]
    return boundary_dofs, boundary_coords

WIDTH, HEIGHT = 0.1, 1 
NX, NY = 4, 26

domain = create_rectangle(
    MPI_COMM,
    [np.array([-WIDTH/2, 0]), np.array([WIDTH/2, HEIGHT])],
    [NX, NY],
    cell_type=CellType.quadrilateral,
)

V = dfx.fem.functionspace(domain, ("P", 2, shape))
fdim = domain.geometry.dim - 1

def boundary(x):
    return np.logical_or((np.abs(x[1] - HEIGHT) < tol) , np.abs(np.abs(x[0]) - WIDTH / 2) < tol)

coupling_boundary = dfx.mesh.locate_entities_boundary(domain, fdim, boundary)
boundary_tags = dfx.mesh.meshtags(domain, fdim, np.sort(coupling_boundary), 1)

boundary_dofs, boundary_coords = interpolation_points_in_vector_space(V, boundary_tags)
with open(f"interpolation_points.csv", "w") as p_file:
    p_file.write("X,Y,Z\n")
    np.savetxt(p_file, boundary_coords, delimiter=",")

which givme the interpolation points coordinates in the boundary, see the small dots in the image, notice the function space is 2nd degree.

now my question is, if is OK to setup values to that points using this method, in the solve loop:

f = dfx.fem.Function(V)

while True:
    ...
    f.vector[boundary_dofs] =  read_data.flatten()
    f.vector.assemble()
    problem.solve()

Or I need something else.

[dokken]

It is almost alright. However, as you are using a vector space (blocked), you will observe that there is only a single coordinate for each dof location, while you would like to set data to both the x and y component.

To do so you need to unroll:

@Eduardo_Firvida

boundary_dofs = dfx.fem.locate_dofs_topological(V, fdim, tags)
    boundary_coords = fs_coords[boundary_dofs]

Once accessed.

Dofs in blocked spaces are ordered as

(Dof0_x, Dof0_y, Dof1_x, Dof1_, ……)
This means that you need to make a loop

bs = V.dofmap.bs
unrolled_dofs = np.empty(len(boundary_dofs)*bs,dtype=np.int32)

unrolled_coords = np.empty((len(boundary_dofs)*bs,3),dtype=np.int32)

for (i, dof) in enumerate(boundary_dofs):
    for b in range(bs):
        unrolled_dofs[i*bs+b] = dof*bs+b
        unrolled_coords[i*bs+b] = fs_coords[i]

I typed this up on my phone, so there might be typos (and it could be vectorized with numpy), but hopefully you get the general idea.

[Eduardo_Firvida]

I really don’t undestand your answer can you please explain it better. Because maybe here is where my mistake is, I’m having bad result, but this is maybe for another dedicated thread.

I don-t know what you mean with bloqued Vector Space, an unrolled dof/coords. As I investigate V.tabulate_dof_coordinates() givme all coords of de dof. And with the locate_dofs_topological i get the dof indices. As I plot in my previous post, I plot that X,Y coords of the dof and they seems to be OK.

Now I’m not sure about the mapping data back to the function. Here in the context of this code snippet:

f = dfx.fem.Function(V)

while True:
    ...
    f.vector[boundary_dofs] =  read_data.flatten()
    f.vector.assemble()
    problem.solve()

read_data is an array of loads with shape N*dim so I flatten that array I think I have the data in the rigth shape of the vector data. So If I understand what you say is that the boundary_dof of my snippets have to be something like [1,1,2,2,…N,N] to correct map the Fx,Fy of the same dof?

If is this what you mean, I have some updates on that context, where I did something like:

1 - use PETSc instead of np.array

vector_size = len(V.tabulate_dof_coordinates().flatten())
bs = V.dofmap.bs

vector = PETSc.Vec().createMPI(vector_size, comm=PETSc.COMM_WORLD)
vector.setFromOptions()
vector.setUp()

2- use array to map the incoming data (read_data) with every dof in the vector space in the right shape

arr = vector.getArray()
arr = arr.reshape(-1, bs)
arr[boundary_dofs] = read_data

3- set the value to the PETCs vector, hopefully this will works in parallel

start, end = vector.getOwnershipRange()
vector[start:end] = arr[start:end]
vector.assemble()

4- the put the received data into the f Function, to solve the elastic problem

f = Function(V, name="Force")
vector.copy(f.vector)
f.vector.assemble()
f.x.scatter_forward()

[dokken]

Consider the following minimal example:

from mpi4py import MPI
import dolfinx

mesh = dolfinx.mesh.create_unit_square(MPI.COMM_WORLD, 1, 1)
shape = (2,)
V = dolfinx.fem.functionspace(mesh, ("P", 2, shape))

x = V.tabulate_dof_coordinates()
print(x.shape, mesh.geometry.x.shape)
u = dolfinx.fem.Function(V)
print(len(u.x.array))

Here we create a 1x1 mesh, with 4 vertices.
We create a second order function space, i.e. there will be dofs in 9 locations in the mesh.
However, as we have created a blocked space with shape (2, ) the array u will have 18 dofs.
This is seen by the print:

(9, 3) (4, 3)
18

Let’s next locate the dofs on the lower boundary. They will be in 3 distinct places, but there will be 6 dofs:

import numpy as np

boundary_facets = dolfinx.mesh.locate_entities_boundary(
    mesh, mesh.topology.dim - 1, lambda x: x[1] < 1e-10
)
boundary_dofs = dolfinx.fem.locate_dofs_topological(
    V, mesh.topology.dim - 1, boundary_facets
)
print(boundary_facets, boundary_dofs)

As we can see by this output, boundary dofs only have three entries, as they are blocked.

[0] [0 1 5]

We can now unroll the degrees of freedom, as shown earlier:

bs = V.dofmap.bs
unrolled_dofs = np.empty(len(boundary_dofs) * bs, dtype=np.int32)

unrolled_coords = np.empty((len(boundary_dofs) * bs, 3), dtype=np.float64)

for i, dof in enumerate(boundary_dofs):
    for b in range(bs):
        unrolled_dofs[i * bs + b] = dof * bs + b
        unrolled_coords[i * bs + b] = x[dof]
print(unrolled_dofs, unrolled_coords)

NOTE: I made some minor mistakes in the previous code that I wrote on my phone, and here is the corrected version that yields:

[ 0  1  2  3 10 11] [[ 2.15422807e-17  2.15422807e-17  0.00000000e+00]
 [ 2.15422807e-17  2.15422807e-17  0.00000000e+00]
 [ 1.00000000e+00 -2.15422807e-17  0.00000000e+00]
 [ 1.00000000e+00 -2.15422807e-17  0.00000000e+00]
 [ 5.00000000e-01  0.00000000e+00  0.00000000e+00]
 [ 5.00000000e-01  0.00000000e+00  0.00000000e+00]]

[Eduardo_Firvida]

Thank for yout quick response, Now I understand what you mean, but I dont know this is applicable to my case. Because Now I cant map my data because they have different shapes

consider this example based on yours.

# generate randome data for all the vector space
read_data = np.random.random(unrolled_coords.shape)
# give u function values in the selected dof
u.vector[unrolled_dofs] = read_data

but here u.vector[unrolled_dofs] hace shape (6) and read_data is (6,3) so now how can I give those values to the dofs?

[dokken]

@Eduardo_Firvida

read_data = np.random.random(unrolled_coords.shape

read data should now only by a (6, ) array, as the dof coordinates for each direction is duplicated, which was the whole point of unrolling them.