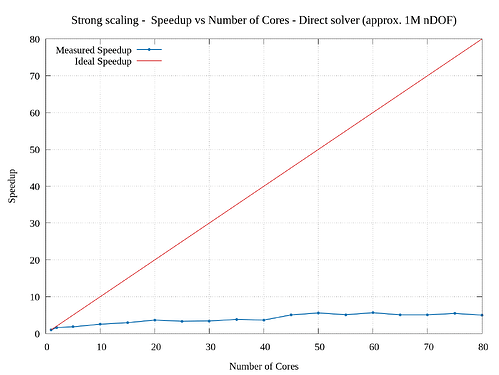
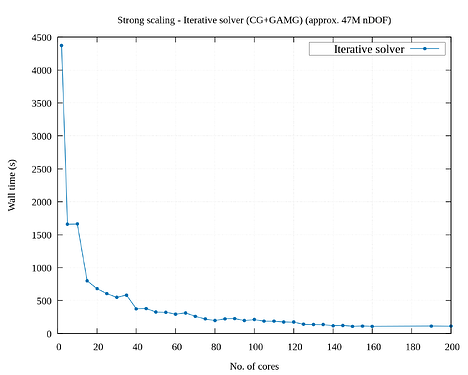
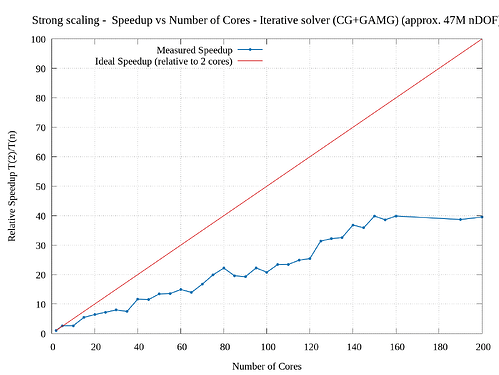
I’m trying to study the parallel scalability of a 3D linear elasticity problem. I’m observing poor scalability when increasing the number of cores. I tried to use a direct solver (solving approx. 1M nDOF) as well an iterative solver (solving approx. 47M nDOF) and obtained sub-par parallelization efficiency. I have attached the corresponding strong scaling results. From the graphs, the speed up for direct solver is very poor. (I have tried a smaller problem for testing the direct solver because of its memory constraints.)
I have already added export OMP_NUM_THREADS=1 in my .bashrc accoring to the post Running in parallel slower than serial?
I am using FEniCSx v0.8.0 through conda both on a cluster and on a work station.
I have used mpirun for running in parallel.
The code (modified from Dokken’s linear elasticity tutorial) used by me for arriving at these results is:
import numpy as np
import ufl
from dolfinx import fem,io,mesh
import dolfinx.fem.petsc
from petsc4py.PETSc import ScalarType
from mpi4py import MPI
start = MPI.Wtime()
# cube mesh 1m x 1m ; 250³ ~ 47M nDOF ; 70³ ~ 1M nDOF
dmesh = mesh.create_unit_cube(MPI.COMM_WORLD, 70, 70, 70, cell_type=mesh.CellType.hexahedron)
V = fem.functionspace(dmesh,("Lagrange", 1, (3,)))
u = ufl.TrialFunction(V)
du = ufl.TestFunction(V)
lmda, mu, K = 121.154e9, 80.77e9, 175e9 # in Pa
def left(x):
return np.isclose(x[0],0)
def right(x):
return np.isclose(x[0],1.0)
left_facets = mesh.locate_entities_boundary(dmesh, 2, left)
left_dofs = fem.locate_dofs_topological(V, 2, left_facets)
u_right = fem.Constant(dmesh,ScalarType([0.0, 0.0, 0.0]))
right_facets = mesh.locate_entities_boundary(dmesh, 2, right)
right_dofs = fem.locate_dofs_topological(V, 2, right_facets)
bc_right = fem.dirichletbc(u_right, right_dofs, V)
bc_left = fem.dirichletbc(np.array([0.0,0.0,0.0],dtype=ScalarType), left_dofs, V)
marked_facets = np.hstack([left_facets, right_facets])
marked_values = np.hstack([np.full_like(left_facets, 1), np.full_like(right_facets, 2)])
sorted_facets = np.argsort(marked_facets)
facet_tag = mesh.meshtags(dmesh, 2, marked_facets[sorted_facets], marked_values[sorted_facets])
t_bar = fem.Constant(dmesh,ScalarType([0.0, 0.0, 0.0]))
b = fem.Constant(dmesh,np.array([0.0,0.0,0.0],dtype=ScalarType))
ds = ufl.Measure(integral_type="ds", domain=dmesh, subdomain_data=facet_tag , subdomain_id=2)
# constitutive and kinematical relations
def sigma(u):
return (lmda * ufl.tr(epsilon(u)) * ufl.Identity(len(u))) + (2 * mu * epsilon(u))
def epsilon(u):
return 0.5*(ufl.nabla_grad(u)+ufl.nabla_grad(u).T)
# variational form
L = ufl.inner(sigma(u),ufl.grad(du)) * ufl.dx
R = ufl.dot(b,du) * ufl.dx + ufl.dot(t_bar,du) * ds
cffi_options = ["-Ofast"]
jit_options = {"cffi_extra_compile_args": cffi_options,
"cffi_libraries": ["m"] }
# iterative solver
# problem = fem.petsc.LinearProblem(L,R,[bc_left],petsc_options = {"ksp_type": "cg", "pc_type": "gamg"},jit_options=jit_options)
# direct solver
problem = fem.petsc.LinearProblem(L,R,[bc_left],petsc_options={ "ksp_type": "preonly", "pc_type": "lu", "pc_factor_mat_solver_type": "mumps"}, jit_options=jit_options) # (LHS, RHS, [boundary conditions], solver options)
out_u = io.XDMFFile(dmesh.comm,"./results-mechanics_field/deformation.xdmf", "w")
out_u.write_mesh(dmesh)
pseudotimesteps = np.linspace(0,5e9,5)
for i in pseudotimesteps:
t_bar.value = [0.0, -i, 0.0]
displacement = problem.solve()
out_u.write_function(displacement,i)
out_u.close()
end = MPI.Wtime()
time = MPI.COMM_WORLD.reduce(end-start,op=MPI.MAX,root=0)
if (MPI.COMM_WORLD.rank == 0):
print(f" Time for computation: {time} s")
I am beginner in FEniCSx and I want to implement and run complex 3D fracture problems to which scaling behavior is very critical.
Could you please advise me on improving the scaling behavior of the code? and correct me if I am not doing something right.
Thank you for your time!
P.S.: I have applied the traction load in steps to mimic the behavior of load stepping for nonlinear problems (for future). I understand that for the current problem it is not necessary.
I did not get much information from other posts regarding big/very big problems.