Hey everyone
I’m attempting to model an electric machine for now in magnetostatic 2D.
I’m using dolfinx 0.9.0 on WSL 2.
I’m running into an issue where if I excite PhaseA1, the magnetic vector potential is extremely high and not originating form the PhaseA1 surface. If, however, I ignore PhaseA1 and excite any other face, PhaseA2 for example. I do get the result I expect.
A MWE is:
from math import pi
import numpy as np
import pyvista
import ufl
from basix.ufl import element
from dolfinx import default_scalar_type
from dolfinx.fem import functionspace, Constant, Function, form, assemble_scalar, locate_dofs_topological, dirichletbc
from dolfinx.fem.petsc import LinearProblem
from dolfinx.io.gmshio import read_from_msh
from dolfinx.mesh import locate_entities_boundary
from dolfinx.plot import vtk_mesh
from mpi4py.MPI import COMM_WORLD
from ufl import Measure, TrialFunction, TestFunction, inner, grad, as_ufl
class Config:
excitation = {
"current": 250.0,
"current_offset": 0.0,
"turns": 9,
}
geometry = {'Bounds': 15, 'Center': {'center': 1},
'Duct': {'geom': {'curve': [101, 102, 103, 104, 105, 106, 107, 108, 109], 'curve_loop': 22, 'name': 'Duct', 'point': [103, 104, 105, 106, 107, 108, 109, 110, 111], 'surface': [17, 18, 19, 20], 'tag': 10}, 'material': {'mu_0': 4*pi * 1e-7, 'mu_r': 1.0}},
'Lower_band': {'geom': {'curve': [158, 159, 160, 161], 'curve_loop': 44, 'name': 'AirGap_LowerBand', 'point': [140, 142, 144, 146], 'surface': [33], 'tag': 13}, 'material': {'mu_0': 4*pi * 1e-7, 'mu_r': 1.0}},
'Magnet1': {'geom': {'curve': [93, 94, 95, 96], 'curve_loop': 20, 'name': 'Magnet1', 'point': [95, 96, 97, 98], 'surface': [14], 'tag': 11}, 'material': {'mu_0': 4*pi * 1e-7, 'mu_r': 1.03}},
'Magnet2': {'geom': {'name': 'Magnet2', 'surface': [15], 'tag': 12}, 'material': {'mu_0': 4*pi * 1e-7, 'mu_r': 1.03}},
'PhaseA1': {'geom': {'curve': [1, 2, 3, 4], 'curve_loop': 1, 'name': 'PhaseA1', 'point': [2, 3, 4, 5], 'surface': [1], 'tag': 4}, 'material': {'mu_0': 4*pi * 1e-7, 'mu_r': 1.0}},
'PhaseA2': {'geom': {'name': 'PhaseA2', 'surface': [2], 'tag': 5}, 'material': {'mu_0': 4*pi * 1e-7, 'mu_r': 1.0}},
'PhaseB1': {'geom': {'name': 'PhaseB1', 'surface': [5], 'tag': 6}, 'material': {'mu_0': 4*pi * 1e-7, 'mu_r': 1.0}},
'PhaseB2': {'geom': {'name': 'PhaseB2', 'surface': [6], 'tag': 7}, 'material': {'mu_0': 4*pi * 1e-7, 'mu_r': 1.0}},
'PhaseC1': {'geom': {'name': 'PhaseC1', 'surface': [3], 'tag': 8}, 'material': {'mu_0': 4*pi * 1e-7, 'mu_r': 1.0}},
'PhaseC2': {'geom': {'name': 'PhaseC2', 'surface': [4], 'tag': 9}, 'material': {'mu_0': 4*pi * 1e-7, 'mu_r': 1.0}},
'Rotor': {'geom': {'curve': [143, 144, 145, 146], 'curve_loop': 37, 'name': 'Rotor', 'point': [134, 135, 136, 137], 'surface': [32], 'tag': 2}, 'material': {'mu_0': 4*pi * 1e-7, 'mu_r': 1000}},
'Slot': {'geom': {'curve': [25, 26, 27, 28, 29, 30, 31, 32], 'curve_loop': 7, 'name': 'Slot', 'point': [26, 27, 28, 29, 30, 31, 32, 33, 34], 'surface': [8, 9, 10, 11, 12, 13], 'tag': 3}, 'material': {'mu_0': 4*pi * 1e-7, 'mu_r': 1.0}},
'Stator': {'geom': {'curve': [132, 133, 134, 135], 'curve_loop': 29, 'name': 'Stator', 'point': [130, 131, 132, 133], 'surface': [22], 'tag': 1}, 'material': {'mu_0': 4*pi * 1e-7, 'mu_r': 1000}},
'Upper_band': {'geom': {'curve': [162, 163, 164, 165], 'curve_loop': 45, 'name': 'AirGap_UpperBand', 'point': [141, 143, 145, 147], 'surface': [34], 'tag': 14}, 'material': {'mu_0': 4*pi * 1e-7, 'mu_r': 1.0}}}
mesh, cell_tags, facet_tags = read_from_msh("geometry.msh", comm=COMM_WORLD, rank=0, gdim=2)
mesh.topology.create_connectivity(2, 1)
mesh.topology.create_connectivity(1, 2)
mesh.topology.create_connectivity(2, 0)
mesh.topology.create_connectivity(0, 2)
dx = Measure("dx", subdomain_data=cell_tags, domain=mesh, metadata={"quadrature_degree": 2})
cell = mesh.ufl_cell().cellname()
# Define function space
CG_V = element("Lagrange", cell, 2, shape=()) # CG: Continuous Galerkin vector potential (Sized for Az only)
DG_0 = element("DG", cell, 0, shape=()) # DG: Discontinuous Galerkin scalar space
V = functionspace(mesh, CG_V)
V_DG = functionspace(mesh, DG_0)
space = {"VectorPotential": V,
"DiscontinuousScalar": V_DG, }
u = TrialFunction(space["VectorPotential"])
v = TestFunction(space["VectorPotential"])
space["TrialFunction"] = {"VectorPotential": u}
space["TestFunction"] = {"VectorPotential": v}
I = Constant(mesh, Config.excitation["current"] * Config.excitation["turns"])
# Define weak form
nu = Function(space["DiscontinuousScalar"])
for key in geometry.keys():
if key in ["Center", "Bounds"]:
continue
out = geometry[key]
tag = out["geom"]["tag"]-1
out["mu"] = 1.0 / (out["material"]["mu_0"] * out["material"]["mu_r"])
cells = cell_tags.find(tag)
nu.x.array[cells] = np.full_like(cells, out["mu"], dtype=default_scalar_type)
u = space["TrialFunction"]["VectorPotential"] # Vector potential trial function
v = space["TestFunction"]["VectorPotential"] # Vector potential test function
a = nu * inner(grad(u), grad(v)) * dx
# Get current excitation
phase_order = ["PhaseA1", "PhaseA2", "PhaseC1", "PhaseC2", "PhaseB1", "PhaseB2"]
phase_offset = [0.0, 0.0, 2 / 3 * pi, 2 / 3 * pi, -2 / 3 * pi, -2 / 3 * pi]
phase_dir = [1.0, 1.0, -1.0, -1.0, 1.0, 1.0] # Direction of current for each phase
current = []
source_terms = []
v = space["TestFunction"]["VectorPotential"]
for i, phase in enumerate(phase_order):
geom = geometry[phase]["geom"]
coil_I = as_ufl(default_scalar_type(phase_dir[i]) * I) # [A] Current magnitude
pos = as_ufl(default_scalar_type(0)) # [rad] Position of the rotor at the current timestamp
coil_current = coil_I * ufl.cos(pos + phase_offset[i])
cells = cell_tags.find(geom["tag"]-1)
Jz = Function(space["DiscontinuousScalar"])
Jz.x.array[:] = 0
Jz.x.array[cells] = coil_current / assemble_scalar(form(1 * dx(geom["tag"]-1)))
Jz.x.scatter_forward()
from dolfinx import plot
import pyvista
from pyvista import UnstructuredGrid
plotter = pyvista.Plotter(window_size=(500, 500))
topology, cells, x = plot.vtk_mesh(mesh, mesh.topology.dim)
grid = UnstructuredGrid(topology, cells, x)
Jz_val = Jz.x.array
grid.cell_data["Jz"] = Jz_val
plotter.add_mesh(grid, scalars="Jz", show_edges=True, cmap="coolwarm")
plotter.view_xy()
plotter.show()
L = Jz * v * dx
source_terms.append(L)
L = sum(source_terms)
# Boundary conditions
tdim = mesh.topology.dim - 1
facets = locate_entities_boundary(mesh, tdim, lambda x: np.full(x.shape[1], True))
dofs = locate_dofs_topological(V, tdim, facets)
bc = dirichletbc(default_scalar_type(0), dofs, V)
bcs = [bc]
Az = Function(space["VectorPotential"])
problem = LinearProblem(a,
L,
u=Az,
bcs=bcs,
petsc_options={"ksp_type": "preonly",
"pc_type": "lu",
"pc_factor_mat_solver_type": "mumps",
"ksp_error_if_not_converged": True}
)
problem.solve()
plotter = pyvista.Plotter()
Az_grid = pyvista.UnstructuredGrid(*vtk_mesh(space["VectorPotential"]))
Az_grid.point_data["A_z"] = Az.x.array
Az_grid.set_active_scalars("A_z")
warp = Az_grid.warp_by_scalar("A_z", factor=1e-10)
actor = plotter.add_mesh(warp, show_edges=True)
plotter.view_xy()
plotter.show()
With the mesh generated by:
from dataclasses import dataclass
from math import pi, radians, cos, sin, tan, ceil
import gmsh
from sympy import symbols, Eq, solve
mm = 1e-3 # [m] millimeter to meter conversion factor
@dataclass
class MachineDims:
dimension: int = 2 # [int] Dimension of the geometry, 2D or 3D
periodicity: int = 8
geom_start_angle: float = 0.0 # [rad] Start angle of the geometry
geom_end_angle: float = 1/periodicity * 2 * pi # [rad] end angle of the geometry in radians
l_ag: float = 1.5*mm # [m] Radial length of the air gap
slots = 48 # number of slots
@dataclass
class WedgeDims:
r_inner: float
r_outer: float
@dataclass
class StatorDims(WedgeDims):
r_inner: float = 161.90/2*mm
r_outer: float = 269.24/2*mm
@dataclass
class RotorDims(WedgeDims):
r_inner: float = 110.64/2*mm
r_outer: float = 160.40/2*mm
@dataclass
class SlotDims:
a_slot_gap = radians(1.366) # [rad]
h_tooth_tip = 1.03*mm # [m] height of the tooth tip
w_tooth_tip = 1.535*mm # [m] width of the tooth tip
h_slot = 29.50*mm # [m] height of the slot
a_slot_widening = radians(1.25) # [rad] angle of the slot widening
h_insulation = 3.50*mm # [m] height of the insulation
@dataclass
class DuctDims:
a_duct = 65.0 / 180 * pi # [rad]
r_duct_maximum = 78.72*mm # [m]
r_duct_minimum = 62.6*mm # [m]
h_duct = 4.7*mm # [m]
o_magnet = 2.25*mm # [m] offset of the magnet from the mirror plane
h_magnet = 6.48*mm # [m] height of the magnet
w_magnet = 16.0*mm # [m] width of the magnet
w_duct_peak = 3.0*mm # [m] width of the duct peak
def mirror_entities(entities, angle, point=(0,0,0)):
"""
Mirror a list of entities across a plane defined by a normal vector and a point.
:param entities: List of entities to be mirrored.
:param angle: Angle to the plane to the x-axis.
:param point: A point on the plane across which to mirror.
:return: List of mirrored entities.
"""
a = sin(angle)
b = -cos(angle)
c = 0
d = -(a * point[0] + b * point[1] + c * point[2])
e = factory.copy(entities)
factory.mirror(e, a, b, c, d)
return e
def repeat_shape_on_angle(out: list, slots: int = None, periodicity: int = None, angle: float = None) -> list:
"""
Repeat a shape defined in out[0] around the z-axis at an angle defined by the number of slots and periodicity.
:param out: List containing the shape to be repeated.
:param slots: Total number of slots in the machine.
:param periodicity: Number of slots in one period.
:param angle: Specific angle to rotate the shape. If None, it will be calculated based on slots and periodicity.
:return: List of entities after rotation.
"""
if slots is not None and periodicity is not None:
out_new = [out[0][1]]
for i in range(1, ceil(slots/periodicity)):
angle = i * (2 * pi / slots)
rotated_surface = factory.copy([out[0]])
factory.rotate(rotated_surface, 0, 0, 0, 0, 0, 1, angle)
out_new.append(rotated_surface[0][1])
elif angle is not None:
rotated_surface = factory.copy([out[0]])
factory.rotate(rotated_surface, 0, 0, 0, 0, 0, 1, angle)
out_new = [rotated_surface[0][1]]
else:
raise ValueError("Either angle or both slots and periodicity must be provided.")
return out_new
def cut_from_surface(out: list, tool_surfaces: list) -> list:
"""
Cut the tool surfaces from the output surface.
:param out: List containing the surface to be cut.
:param tool_surfaces: List of surfaces to be used as tools for cutting.
:return: List of entities after cutting.
"""
surfaces_to_cut = [(2, surface) for surface in tool_surfaces]
cut_result, _ = factory.cut([(2, out[0])], surfaces_to_cut, removeObject=False, removeTool=False)
return [tag for dim, tag in cut_result if dim == 2] # Keep only the surface tags
def square_in_polar_coordinates(r1, r2, a1, a2) -> tuple:
"""
Create a square in polar coordinates defined by two radii and two angles.
:param r1: Inner radius of the square.
:param r2: Outer radius of the square.
:param a1: Start angle of the square.
:param a2: End angle of the square.
:return: List of points defining the square in polar coordinates.
"""
x = [r1 * cos(a1), r1 * cos(a2), r2 * cos(a2), r2 * cos(a1)]
y = [r1 * sin(a1), r1 * sin(a2), r2 * sin(a2), r2 * sin(a1)]
z = [0, 0, 0, 0] # All points are in the same plane (z=0)
return x, y, z
def draw_square_from_points(out: dict) -> dict:
"""
Draw a square from the points defined in the out dictionary.
:param out: dictionary containing the points of the square.
:return: dictionary containing the points, curves, curve loop, and surface of the square.
"""
out["curve"].extend([
factory.addLine(out["point"][0], out["point"][1]), # Bottom line
factory.addLine(out["point"][1], out["point"][2]), # Right line
factory.addLine(out["point"][2], out["point"][3]), # Top line
factory.addLine(out["point"][3], out["point"][0]) # Left Line
])
# Create the curve loop and surface for the magnet
out["curve_loop"] = factory.addCurveLoop(out["curve"])
out["surface"] = [factory.addPlaneSurface([out["curve_loop"]])]
return out
def solve_algebraic_system(param, eq1, eq2) -> tuple[float, float]:
"""
Solve a system of algebraic equations.
:param param: The parameters to solve for, typically a tuple of symbols.
:param eq1: First equation in the system.
:param eq2: Second equation in the system.
:return: A tuple containing the solutions for x and y.
"""
solutions = solve((eq1, eq2), param)
if solutions[0][0] > 0 and solutions[0][1] > 0:
return solutions[0]
else:
return solutions[1]
gmsh.initialize()
gmsh.model.add("GeometryBuilder")
machine_dims = MachineDims()
stator_dims = StatorDims()
rotor_dims = RotorDims()
slot_dims = SlotDims()
duct_dims = DuctDims()
## Build the geometry
factory = gmsh.model.occ
out = {}
# Create the center point
center_tag = factory.addPoint(0, 0, 0, 1e-2)
out['center'] = center_tag
coil_out = {"point": [], "curve": [], "curve_loop": None, "surface": []}
slots = machine_dims.slots # Number of slots in the machine
a_slot_gap = slot_dims.a_slot_gap # Angle of the slot gap
h_tooth_tip = slot_dims.h_tooth_tip # Height of the tooth tip
h_slot = slot_dims.h_slot # Height of the slot
h_insulation = slot_dims.h_insulation # Height of the insulation
r1 = stator_dims.r_inner + h_tooth_tip + h_insulation
r2 = stator_dims.r_inner + h_tooth_tip + h_slot
a1 = machine_dims.geom_start_angle + (2*pi / slots) / 2 - a_slot_gap
a2 = machine_dims.geom_start_angle + (2*pi / slots) / 2 + a_slot_gap
# Calculate the coordinates of the coil points
x, y, z = square_in_polar_coordinates(r1, r2, a1, a2)
for i in range(len(x)):
point_tag = factory.addPoint(x[i], y[i], z[i], 1e-3)
coil_out["point"].append(point_tag)
coil_out = draw_square_from_points(coil_out)
coils = {"PhaseA1": coil_out,
"PhaseA2": {"surface": []},
"PhaseC1": {"surface": []},
"PhaseC2": {"surface": []},
"PhaseB1": {"surface": []},
"PhaseB2": {"surface": []}}
# Repeat the coil surface for all slots
for i, coil in enumerate(coils.keys()):
if coil == "PhaseA1":
coils[coil]["name"] = coil
continue
coils[coil]["surface"] = repeat_shape_on_angle([(2, coil_out["surface"][0])], angle=i * (2 * pi / slots))
coils[coil]["name"] = coil
coil_out = coils
slot_out = {"point": [], "curve": [], "curve_loop": None, "surface": []}
slots = machine_dims.slots # Number of slots in the machine
periodicity = machine_dims.periodicity # Periodicity of the machine geometry
a_slot_gap = slot_dims.a_slot_gap # Angle of the slot gap
h_tooth_tip = slot_dims.h_tooth_tip # Height of the tooth tip
w_tooth_tip = slot_dims.w_tooth_tip # Width of the tooth tip
h_slot = slot_dims.h_slot # Height of the slot
a_slot_widening = slot_dims.a_slot_widening # Angle of the slot widening
r1 = stator_dims.r_inner # Inner radius of the stator
r2 = stator_dims.r_inner + h_tooth_tip
r4 = stator_dims.r_inner + h_tooth_tip + h_slot - 1e-4
a1 = machine_dims.geom_start_angle + (2*pi / slots) / 2 - a_slot_gap # Start angle of the slot
a2 = a1 - 1/2*pi
a3 = a2 - a_slot_widening
a4 = machine_dims.geom_start_angle + (2*pi / slots) / 2
# Calculate the coordinates of the slot points
x = [r1*cos(a1), r2*cos(a1), r2*cos(a1) + w_tooth_tip*cos(a2), r2*cos(a1) + w_tooth_tip*cos(a2) - h_slot*sin(a3), r4*cos(a4),]
y = [r1*sin(a1), r2*sin(a1), r2*sin(a1) + w_tooth_tip*sin(a2), r2*sin(a1) + w_tooth_tip*sin(a2) + h_slot*cos(a3), r4*sin(a4),]
z = [0] * len(x)
for i in range(len(x)):
point_tag = factory.addPoint(x[i], y[i], z[i], 1e-3)
slot_out["point"].append(point_tag)
# Repeat the points on the other half of the slot
points = [(0, x) for x in slot_out["point"][0:-1][::-1]]
mirrored_points = mirror_entities(points, angle=a4, point=(0, 0, 0))
slot_out["point"].extend([x[1] for x in mirrored_points])
# Create the curves for the slot
slot_out["curve"].extend([
factory.addLine(slot_out["point"][0], slot_out["point"][1]), # Inner line
factory.addLine(slot_out["point"][1], slot_out["point"][2]), # Tooth tip line
factory.addLine(slot_out["point"][2], slot_out["point"][3]), # Slot wall
factory.addCircleArc(slot_out["point"][3], slot_out["point"][4], slot_out["point"][5]), # Outer arc
factory.addLine(slot_out["point"][5], slot_out["point"][6]), # Slot wall
factory.addLine(slot_out["point"][6], slot_out["point"][7]), # Tooth tip line
factory.addLine(slot_out["point"][7], slot_out["point"][8]), # Inner line
factory.addLine(slot_out["point"][8], slot_out["point"][0])]) # Closing line
# Create the curve loop and surface for the slot
slot_out["curve_loop"] = factory.addCurveLoop(slot_out["curve"])
slot_out["surface"] = [factory.addPlaneSurface([slot_out["curve_loop"]])]
# Cut the coil out of the slot surface
if coil_out is not None:
for key, coil_surface in coil_out.items():
slot_out["surface"].append(cut_from_surface(slot_out["surface"], coil_surface["surface"])[0])
old_surface = slot_out["surface"][0]
factory.remove([(2, old_surface)], recursive=True)
slot_out["surface"] = slot_out["surface"][1:]
# Repeat the slot surface for all slots
slot_out["surface"] = repeat_shape_on_angle([(2, slot_out["surface"][0])], slots, periodicity)
slot_out["name"] = "Slot"
stator_out = {"point": [], "curve": [], "curve_loop": None, "surface": []}
r1 = stator_dims.r_inner # Inner radius of the stator
r2 = stator_dims.r_outer # Outer radius of the stator
a1 = machine_dims.geom_start_angle # Start angle of the geometry
a2 = machine_dims.geom_end_angle # End angle of the geometry
# Create the points for the stator
x, y, z = square_in_polar_coordinates(r1, r2, a1, a2)
for i in range(4):
point_tag = factory.addPoint(x[i], y[i], z[i], 1e-3)
stator_out["point"].append(point_tag)
# Create the curves for the wedge
stator_out["curve"].append(factory.addCircleArc(stator_out["point"][0], 1, stator_out["point"][1])) # Inner arc
stator_out["curve"].append(factory.addLine(stator_out["point"][1], stator_out["point"][2])) # Start Line
stator_out["curve"].append(factory.addCircleArc(stator_out["point"][2], 1, stator_out["point"][3])) # Outer arc
stator_out["curve"].append(factory.addLine(stator_out["point"][3], stator_out["point"][0])) # End Line
# Create the curve loop and surface for the stator
stator_out["curve_loop"] = factory.addCurveLoop(stator_out["curve"])
stator_out["surface"] = [factory.addPlaneSurface([stator_out["curve_loop"]])]
surface_to_cut = [slot_out, coil_out]
if not isinstance(surface_to_cut, list):
surface_to_cut = [surface_to_cut]
for surface_tc in surface_to_cut:
if "PhaseA1" in surface_tc.keys():
for key, coil_surface in surface_tc.items():
if "surface" in coil_surface:
stator_out["surface"] = cut_from_surface(stator_out["surface"], coil_surface["surface"])
else:
raise ValueError(f"Coil {key} does not contain a surface to cut from the slot.")
elif surface_tc["name"] in {"Slot"}:
name = "Stator"
stator_out["surface"] = cut_from_surface(stator_out["surface"], surface_tc["surface"])
stator_out["name"] = name
gmsh.model.occ.synchronize()
geometry = {"Center": out,
"Stator": {"geom": stator_out},
"Slot": {"geom": slot_out},
"PhaseA1": {"geom": coils["PhaseA1"]},
"PhaseA2": {"geom": coils["PhaseA2"]},
"PhaseB1": {"geom": coils["PhaseB1"]},
"PhaseB2": {"geom": coils["PhaseB2"]},
"PhaseC1": {"geom": coils["PhaseC1"]},
"PhaseC2": {"geom": coils["PhaseC2"]}}
for key in geometry.keys():
if key in ["Center", "Bounds"]:
continue
out = geometry[key]["geom"]
out["tag"] = gmsh.model.addPhysicalGroup(2, out["surface"])
gmsh.model.setPhysicalName(2, out["tag"], out["name"])
gmsh.model.mesh.generate(2)
gmsh.write("geometry.msh")
gmsh.fltk.run()
gmsh.finalize()
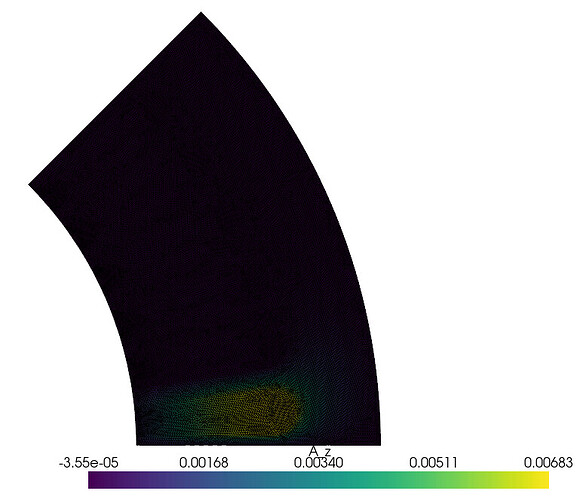
If I run this code, the magnetic vector potential shows:
Editing the code slightly, removing coil excitation in PhaseA1 by changing
phase_order = ["PhaseA1", "PhaseA2", "PhaseC1", "PhaseC2", "PhaseB1", "PhaseB2"]
to
phase_order = ["PhaseA2", "PhaseC1", "PhaseC2", "PhaseB1", "PhaseB2"]
gives:
I have checked the excitation Jz for phase A1:
which is equal to phase A2 in magnitude, but located in region A1, as one would expect.
Any ideas what could cause this behavior?