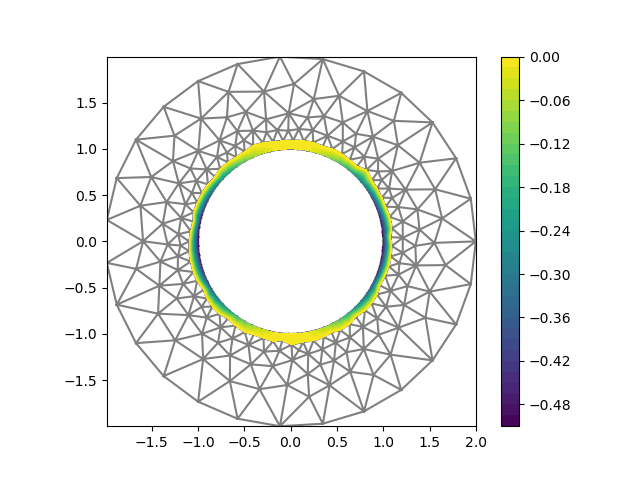
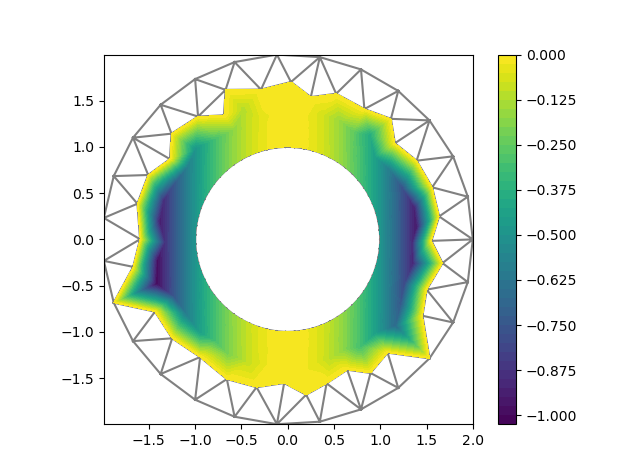
I am using GMSH to produce a sequence of meshes of an annulus (centered at 0, inner radius 1, outer radius 2), with greater resolution on the inner circle to get better accuracy:
I am solving a poisson equation with exact solution u_ex = 0 if x[0]<=0, x[0]**2 otherwise, Dirichlet BCs on the inner ring, Neumann on the outer ring.
Computing the achieved order of convergence (L2 norm) yields: [ 3.04670631 -0.08825267 2.56832882 2.30941509 1.64144749 0.59804678 2.70940579], which oscillates a lot (the solution is H2 regular). A similar behaviour is obtained with Dirichlet BCs everywhere.
What could be the explanation for this? Is it a problem of the imposition of the boundary conditions?
Thank you in advance…
Let me post the relevant code, mesh generation comes below:
# %% Some data (e.g. exact solution and what not)
# Mesh path
mesh_path = "/home/annulus/"
# Resolutions
resolutions = [0.2, .1, .05, .025, .0125, 0.00625, 0.003125] # mesh width array
# Exact solution and corresponding source
class solution(UserExpression):
def __init__(self, **kwargs):
""" Construct the source function """
super().__init__(self, **kwargs)
def eval(self, values, x):
""" Evaluate the source function """
if x[0] >= 0:
values[0] = -x[0] ** 2 / 2
else:
values[0] = 0
class source(UserExpression):
def __init__(self, **kwargs):
""" Construct the source function """
super().__init__(self, **kwargs)
def eval(self, values, x):
""" Evaluate the source function """
if x[0] >= 0:
values[0] = 1
else:
values[0] = 0
class normal_derivative(UserExpression):
def __init__(self, **kwargs):
super().__init__(self, **kwargs)
def eval(self, values, x):
if x[0] >= 0:
if x[0] ** 2 + x[1] ** 2 < 1.5 ** 2:
values[0] = + x[0]**2
else:
values[0] = - x[0]**2 / 2
else:
values[0] = 0
u_ex = solution()
f = source()
f_D = solution() # Dirichlet BC
f_N = normal_derivative() # Neumann BC
# %% Read that mesh
def read_mesh(resolution, mesh_path=mesh_path):
# The volumetric mesh
mesh = Mesh()
with XDMFFile(mesh_path + "mesh_" + str(resolution) + ".xdmf") as infile:
infile.read(mesh)
# The boundary conditions
mvc = MeshValueCollection("size_t", mesh, 1)
with XDMFFile(mesh_path + "facet_mesh_" + str(resolution) + ".xdmf") as infile:
infile.read(mvc, "name_to_read")
mf = MeshFunctionSizet(mesh, mvc) # remember, tag 3 is inner ring, tag 2 outer ring
L1 = FiniteElement("Lagrange", mesh.ufl_cell(), 1)
V = FunctionSpace(mesh, L1)
return mesh, mf, V
# %% The problem
def solve_single_pb(resolution):
(mesh, mf, V) = read_mesh(resolution)
plot(mesh)
plt.show()
U = TrialFunction(V)
v = TestFunction(V)
# Functional formulation
dOuterRing = Measure("ds", subdomain_data=mf, subdomain_id=2)
F = inner(grad(U), grad(v)) * dX - f_N * v * dOuterRing - f * v * dX
a, L = lhs(F), rhs(F)
# Boundary conditions
bcs = [DirichletBC(V, f_D, mf, 3)] # inner ring, outer ring has already Neumann BCs
u = Function(V)
solve(a == L, u, bcs)
err = errornorm(u_ex, u)
return err
# %% Error checking
err_vec = []
for res in resolutions:
err_vec.append(solve_single_pb(res))
err_vec = np.array(err_vec)
ooc = -np.log2( err_vec[1:]/err_vec[:-1])
print(ooc)
And here, the mesh generation code:
# %%
resolution = .0125/8
# An empty geometry
geometry = pygmsh.geo.Geometry()
# Create a model to add data to
model = geometry.__enter__()
# A circle centered at the origin and radius 1
circle = model.add_circle([0.0, 0.0, 0.0], 2.0, mesh_size=5*resolution) # meshes are always 3D, I will suppress the third component in case
# A hole
hole = model.add_circle([0.0, 0.0, 0.0], 1.0, mesh_size=1*resolution)
# My surface
plane_surface = model.add_plane_surface(circle.curve_loop,[hole.curve_loop])
# Sinchronize, before adding physical entities
model.synchronize()
#%%
# Tagging/marking boundaries and volume.
# Boundaries with the same tag should be added simultaneously
model.add_physical([plane_surface], "volume")
model.add_physical(circle.curve_loop.curves, "outer_ring")
model.add_physical(hole.curve_loop.curves, "inner_ring")
# Generate the mesh
geometry.generate_mesh(dim=2)
geometry.save_geometry(path+"annulus_"+str(resolution)+".geo_unrolled")
gmsh.write(path+"mesh_"+str(resolution)+".msh")
gmsh.clear()
geometry.__exit__()
#%%##########################
# Saving to a better format #
#############################
mesh_from_file = meshio.read(path+"mesh_"+str(resolution)+".msh")
def create_mesh(mesh, cell_type, prune_z = False):
cells = mesh.get_cells_type(cell_type) # get the cells of some type: it will change!
cell_data = mesh.get_cell_data("gmsh:physical", cell_type)
points = mesh.points[:,:2] if prune_z else mesh.points
out_mesh = meshio.Mesh(points=points, cells={cell_type: cells}, cell_data={"name_to_read":[cell_data]})
return out_mesh
# Using the above function, create line and "plane" mesh
line_mesh = create_mesh(mesh_from_file, "line", prune_z=True)
meshio.write(path+"facet_mesh_"+str(resolution)+".xdmf", line_mesh)
triangle_mesh = create_mesh(mesh_from_file, "triangle", prune_z=True)
meshio.write(path+"mesh_"+str(resolution)+".xdmf", triangle_mesh)