Periodic BC Problem in 3D

1

Hello everyone,

I have a weird issue while using periodic BC in 3D. I have a Box structure and I tried to apply PBC front-back and left-right faces. It seems like it works well for those faces but the problem occurs on corners and sometime on shared edges. The exegerated view of the mesh after loading is given below.

class PeriodicBoundary(SubDomain):
    def inside(self, y, on_boundary):
    #left and front boundary are target domain
        return bool((near(y[0],0) and on_boundary) \
            or (near(y[1],0,tol1) and on_boundary)) \
            and (not(near(y[0],L) or near(y[1],L)))
    def map(self,x,y):
    #map right and back boundary to target domain
        if near(x[0], L):
            y[0] = x[0] - L
            y[1] = x[1]
            y[2] = x[2]
        elif near(x[1], L):
            y[0] = x[0]
            y[1] = x[1] - L
            y[2] = x[2]
        else:
            y[0] = -1000
            y[1] = -1000
            y[2] = -1000

CaptureBox
CaptureBox725×483 206 KB

How can I also define PBC condition for corners and shared edges ? Thank you.

2

Hi CMA,
Could you post a minimum working example with the mesh and the loads that result in this (surprising) image, please ?
Regards,
Baptiste

3

Hello bd1747,

I have already given the definition of periodic BC that i use. Periodic definitions of corner nodes and shared edges should have described into that somehow. It is not related with loading.

More visually, I suspect the following issue:
image

The green edge is shared by blue face and red face. But while defining the periodicity I select the face-wise. And probably one of the face overwrite its condition to other on green edge. Therefore this edge does not show periodicity both in X and Y. It only shows periodicity over one of the axis due to overwrite issue. How can I fix the problem ?

4

Hi CMA,

As you suggest, your problem likely is due to incorrectly dealing with the green edge (although it’s impossible for me to verify this without a minimum working example). In short, you need to include an additional condition in your map function to deal specifically with the case when x=y=L. See e.g. this post on the old FEniCS Q&A site. You should modify your code to something like:

class PeriodicBoundary(SubDomain):
    def inside(self, y, on_boundary):
        #left and front boundary are target domain
        return bool((near(y[0],0) and on_boundary) \
            or (near(y[1],0,tol1) and on_boundary)) \
            and (not(near(y[0],L) or near(y[1],L)))
    def map(self,x,y):
        #map right and back boundary to target domain
        if near(x[0], L) and near(x[1], L):
            # Added this condition to deal with the
            # case x = y = L
            y[0] = x[0] - L
            y[1] = x[1] - L
            y[2] = x[2]
        elif near(x[0], L):
            y[0] = x[0] - L
            y[1] = x[1]
            y[2] = x[2]
        elif near(x[1], L):
            y[0] = x[0]
            y[1] = x[1] - L
            y[2] = x[2]
        else:
            y[0] = -1000
            y[1] = -1000
            y[2] = -1000

Good luck.

Regards,
Connor

5

Hello conpierce8,

Thank you for your suggestion. It works well but i could not get the logic behind the definition. If someone explains that would be great.

Regards

6

Hi CMA,

I’m glad this worked for you! I’ll attempt to explain the logic with references to the following figure:

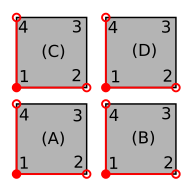
periodicity_simple

In this picture I’ve sketched out four neighboring cells of our periodic system, and I’ve added a space between the unit cells to hopefully clarify the explanation. Consider that we have modeled and meshed cell (A) and we need to define the periodic boundary condition on this cell. We need to create an inside function to identify the minimum set of DOFs needed to model the entire boundary (shown in red in the image), and the map function to map the remaining DOFs to the minimum set. Note that the filled circle indicates point A1 is part of the boundary that we want to retain, while the hollow circles indicate that points A2 and A4 are not part of the boundary that we want to retain.

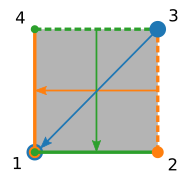
We can see from the illustration that point A3 is the same as point D1. (To see why this is so, imagine that you remove the space between the unit cells.) Therefore, to define a periodic boundary in unit cell A, we need to map point 3 to point 1. Furthermore, all points on edge A2-A3 (excluding point A3) are the same as the points on edge B1-B4, so in unit cell (A) we map edge 2-3 to edge 1-4. Likewise, we map edge 4-3 (excluding point 3) to edge 1-2. Visually, our map looks like this:

periodicity_map

To implement this in code, I used a three-case if-elif-elif-else structure (please see the updated comments in the code which explain what each case does):

    def map(self,x,y):
        #map right and back boundary to target domain
        if near(x[0], L) and near(x[1], L):
            # "x" is located at point 3. Therefore, we must
            # map "x" by -L in *both* the x- and y-directions
            y[0] = x[0] - L
            y[1] = x[1] - L
            y[2] = x[2]
        elif near(x[0], L):
            # "x" is not located at point 3, but it lies
            # somewhere on edge 2-3. Therefore, we must
            # map "x" by -L in *only the x-direction*
            y[0] = x[0] - L
            y[1] = x[1]
            y[2] = x[2]
        elif near(x[1], L):
            # "x" is not located at point 3, but it lies
            # somewhere on edge 4-3. Therefore, we must
            # map "x" by -L in *only the y-direction*
            y[0] = x[0]
            y[1] = x[1] - L
            y[2] = x[2]
        else:
            # "x" is not located on the mapped part
            # of the boundary. We map it to a random point
            # off the boundary (although I'm not sure why
            # this is needed).
            y[0] = -1000
            y[1] = -1000
            y[2] = -1000

Hope this clears it up for you. I’m sorry for the slow response. I’ve been busy with finals this week. :weary:

Regards,
Connor

5 Likes
7

Hello Connor,

Thank you so much for your detailed images and explanations. I got the idea !!

Regards