Periodic BC Problem in 3D

6

Hi CMA,

I’m glad this worked for you! I’ll attempt to explain the logic with references to the following figure:

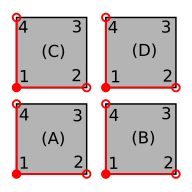
periodicity_simple

In this picture I’ve sketched out four neighboring cells of our periodic system, and I’ve added a space between the unit cells to hopefully clarify the explanation. Consider that we have modeled and meshed cell (A) and we need to define the periodic boundary condition on this cell. We need to create an inside function to identify the minimum set of DOFs needed to model the entire boundary (shown in red in the image), and the map function to map the remaining DOFs to the minimum set. Note that the filled circle indicates point A1 is part of the boundary that we want to retain, while the hollow circles indicate that points A2 and A4 are not part of the boundary that we want to retain.

We can see from the illustration that point A3 is the same as point D1. (To see why this is so, imagine that you remove the space between the unit cells.) Therefore, to define a periodic boundary in unit cell A, we need to map point 3 to point 1. Furthermore, all points on edge A2-A3 (excluding point A3) are the same as the points on edge B1-B4, so in unit cell (A) we map edge 2-3 to edge 1-4. Likewise, we map edge 4-3 (excluding point 3) to edge 1-2. Visually, our map looks like this:

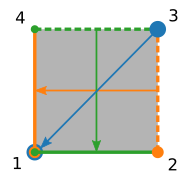
periodicity_map

To implement this in code, I used a three-case if-elif-elif-else structure (please see the updated comments in the code which explain what each case does):

    def map(self,x,y):
        #map right and back boundary to target domain
        if near(x[0], L) and near(x[1], L):
            # "x" is located at point 3. Therefore, we must
            # map "x" by -L in *both* the x- and y-directions
            y[0] = x[0] - L
            y[1] = x[1] - L
            y[2] = x[2]
        elif near(x[0], L):
            # "x" is not located at point 3, but it lies
            # somewhere on edge 2-3. Therefore, we must
            # map "x" by -L in *only the x-direction*
            y[0] = x[0] - L
            y[1] = x[1]
            y[2] = x[2]
        elif near(x[1], L):
            # "x" is not located at point 3, but it lies
            # somewhere on edge 4-3. Therefore, we must
            # map "x" by -L in *only the y-direction*
            y[0] = x[0]
            y[1] = x[1] - L
            y[2] = x[2]
        else:
            # "x" is not located on the mapped part
            # of the boundary. We map it to a random point
            # off the boundary (although I'm not sure why
            # this is needed).
            y[0] = -1000
            y[1] = -1000
            y[2] = -1000

Hope this clears it up for you. I’m sorry for the slow response. I’ve been busy with finals this week. :weary:

Regards,
Connor

5 Likes