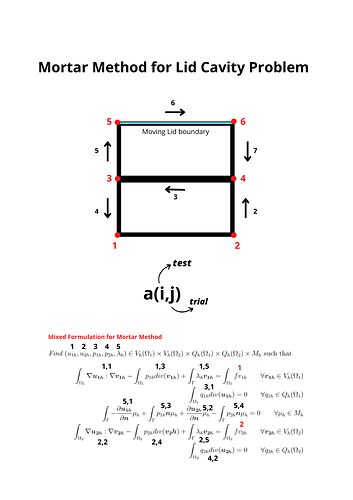
Hi, I have been trying to address Mortar Method for Lid Cavity Problem for a university project using Multifenicsx tools. The problem is defined as in the following picture, I have two subdomains, two variables per subdomain + the lagrange multiplier. I have defined the blocked form a as usual with the indexing reported in the figure and taking into account which trial and test space “talk” to each-other. Anyhow I keep getting a discontinuous type argument error of the following type:
Could you help me find the error in my fenicsx form implementation? Find below the full code.
Thank you in advance
import gmsh
import numpy as np
from dolfinx import fem, plot
import ufl
import dolfinx.io
from dolfinx.io import gmshio
from dolfinx.io import XDMFFile
from mpi4py import MPI
from ufl import div, dx, grad, inner, SpatialCoordinate, FacetNormal
from dolfinx.fem import (Constant, Function, FunctionSpace)
import mpi4py.MPI
import petsc4py.PETSc
import multiphenicsx.fem
import multiphenicsx.io
from petsc4py import PETSc
gmsh.initialize()
gmsh.model.add("mortar")
dim= 0.1
#creation of the down rectangle
gmsh.model.geo.addPoint(0, 0, 0, dim, 1)
gmsh.model.geo.addPoint(1, 0, 0, dim, 2)
gmsh.model.geo.addPoint(0, 0.5, 0, dim, 3)
gmsh.model.geo.addPoint(1, 0.5, 0, dim, 4)
gmsh.model.geo.addPoint(0, 1, 0, dim, 5)
gmsh.model.geo.addPoint(1, 1, 0, dim, 6)
#linking the lines of the rectangles
gmsh.model.geo.addLine(1, 2, 1)
gmsh.model.geo.addLine(2, 4, 2)
gmsh.model.geo.addLine(4, 3, 3) #interface
gmsh.model.geo.addLine(3, 1, 4)
gmsh.model.geo.addLine(3, 5, 5)
gmsh.model.geo.addLine(5, 6, 6) #lid boundary
gmsh.model.geo.addLine(6, 4, 7)
#line between the two rectangles
line= gmsh.model.geo.addLine(3, 4)
#creation of the loops
loop_down= gmsh.model.geo.addCurveLoop([1, 2, 3, 4])
loop_up= gmsh.model.geo.addCurveLoop([3, 5, 6, 7])
#creation of the surface
rect_down= gmsh.model.geo.addPlaneSurface([loop_down])
rect_up= gmsh.model.geo.addPlaneSurface([loop_up])
gmsh.model.geo.synchronize()
gmsh.model.addPhysicalGroup(1, [4, 1, 2], 1) #down boundary physical group
gmsh.model.addPhysicalGroup(1, [3], 2) #interface physical group
gmsh.model.addPhysicalGroup(1, [6], 3) #lid boundary physical group
gmsh.model.addPhysicalGroup(1, [5], 4) #upper left boundary segment
gmsh.model.addPhysicalGroup(1, [7], 5) #upper right boundary segment
gmsh.model.addPhysicalGroup(2, [rect_down], name = "Down rectangle")
gmsh.model.addPhysicalGroup(2, [rect_up], name = "Up rectangle")
gmsh.model.mesh.generate(2)
#mesh, subdomains, boundaries
mesh, subdomains, boundaries = dolfinx.io.gmshio.model_to_mesh(gmsh.model, comm=mpi4py.MPI.COMM_WORLD, rank=0, gdim=2)
gmsh.finalize()
#locate cells in the two subdomains
cells_Omega1 = subdomains.indices[subdomains.values == 1]
cells_Omega2 = subdomains.indices[subdomains.values == 2]
#locate boundary facets
facets_down_boundary = boundaries.indices[boundaries.values == 1]
facets_interface = boundaries.indices[boundaries.values == 2]
facets_lid_boundary = boundaries.indices[boundaries.values == 3]
facets_up_left = boundaries.indices[boundaries.values == 4]
facets_up_right = boundaries.indices[boundaries.values == 5]
#multiphenicsx plot
multiphenicsx.io.plot_mesh(mesh)
multiphenicsx.io.plot_mesh_tags(subdomains)
multiphenicsx.io.plot_mesh_entities(mesh, mesh.topology.dim, cells_Omega1)
multiphenicsx.io.plot_mesh_entities(mesh, mesh.topology.dim, cells_Omega2)
multiphenicsx.io.plot_mesh_tags(boundaries)
multiphenicsx.io.plot_mesh_entities(mesh, mesh.topology.dim - 1, facets_down_boundary)
multiphenicsx.io.plot_mesh_entities(mesh, mesh.topology.dim - 1, facets_interface)
multiphenicsx.io.plot_mesh_entities(mesh, mesh.topology.dim - 1, facets_lid_boundary)
multiphenicsx.io.plot_mesh_entities(mesh, mesh.topology.dim - 1, facets_up_left)
multiphenicsx.io.plot_mesh_entities(mesh, mesh.topology.dim - 1, facets_up_right)
#DEFINITION OF THE MEASURES
# Define associated measures
dx = ufl.Measure("dx")(subdomain_data=subdomains)
dS = ufl.Measure("dS")(subdomain_data=boundaries)
dS = dS(2) # restrict to the interface, which has facet ID equal to 2
n= FacetNormal(mesh)
#DEFINITION OF THE SPACES
# Define function spaces
#We firstly define vector and finite element for upper and lower half of the domain
V1_element = ufl.VectorElement("Lagrange", mesh.ufl_cell(), 2)
Q1_element = ufl.FiniteElement("DG", mesh.ufl_cell(), 1)
W1_element = ufl.MixedElement(V1_element, Q1_element)
W1 = dolfinx.fem.FunctionSpace(mesh, W1_element)
V1, _ = W1.sub(0).collapse()
Q1, _ = W1.sub(1).collapse()
V2_element = ufl.VectorElement("Lagrange", mesh.ufl_cell(), 2)
Q2_element = ufl.FiniteElement("DG", mesh.ufl_cell(), 1)
W2_element = ufl.MixedElement(V2_element, Q2_element)
W2 = dolfinx.fem.FunctionSpace(mesh, W2_element)
V2, _ = W2.sub(0).collapse()
Q2, _ = W2.sub(1).collapse()
#space of the lagrange multiplie
M_element = ufl.VectorElement("Lagrange", mesh.ufl_cell(), 2)
M = dolfinx.fem.FunctionSpace(mesh, M_element)
#define the restrictions
dofs_V1_Omega1 = dolfinx.fem.locate_dofs_topological(V1, subdomains.dim, cells_Omega1) #locate dofs of the V1space
dofs_V2_Omega2 = dolfinx.fem.locate_dofs_topological(V2, subdomains.dim, cells_Omega2) #locate dofs of the V2space
dofs_M_Gamma = dolfinx.fem.locate_dofs_topological(M, boundaries.dim, facets_interface) #locate dofs of the LM space
dofs_Q1_Omega1 = dolfinx.fem.locate_dofs_topological(Q1, subdomains.dim, cells_Omega1) #locate dofs of the Q1space
dofs_Q2_Omega2 = dolfinx.fem.locate_dofs_topological(Q2, subdomains.dim, cells_Omega2) #locate dofs of the Q2space
restriction_V1_Omega1 = multiphenicsx.fem.DofMapRestriction(V1.dofmap, dofs_V1_Omega1)
restriction_V2_Omega2 = multiphenicsx.fem.DofMapRestriction(V2.dofmap, dofs_V2_Omega2)
restriction_Q1_Omega1 = multiphenicsx.fem.DofMapRestriction(Q1.dofmap, dofs_Q1_Omega1)
restriction_Q2_Omega2 = multiphenicsx.fem.DofMapRestriction(Q2.dofmap, dofs_Q2_Omega2)
restriction_M_Gamma = multiphenicsx.fem.DofMapRestriction(M.dofmap, dofs_M_Gamma)
restriction = [restriction_V1_Omega1, restriction_V2_Omega2, restriction_Q1_Omega1, restriction_Q2_Omega2, restriction_M_Gamma]
#DEFINE TRIAL AND TEST FUNCTIONS
(u1, u2, p1, p2, l) = (ufl.TrialFunction(V1), ufl.TrialFunction(V2), ufl.TrialFunction(Q1), ufl.TrialFunction(Q2), ufl.TrialFunction(M))
(v1, v2, q1, q2, m) = (ufl.TestFunction(V1), ufl.TestFunction(V2), ufl.TestFunction(Q1), ufl.TestFunction(Q2), ufl.TestFunction(M))
f = Constant(mesh, (PETSc.ScalarType(0), PETSc.ScalarType(0)))
# Define problem block forms
zero = dolfinx.fem.Constant(mesh, petsc4py.PETSc.ScalarType(0))
a = [[ufl.inner(ufl.grad(u1), ufl.grad(v1)) * dx(1), None, - inner(p1, div(v1)) * dx(1), None, + inner(l,v1)*dS],
[None, ufl.inner(ufl.grad(u2), ufl.grad(v2)) * dx(2), None, - inner(p2, div(v2)) * dx(2), + inner(l,v2)*dS],
[ufl.inner(q1, ufl.div(u1))*dx(1), None, None, None, None],
[None, ufl.inner(q2, ufl.div(u2))*dx(2), None, None, None],
[- ufl.inner(ufl.dot(grad(u1), n),m)*dS, ufl.inner(ufl.dot(grad(u2), n),m)*dS, + ufl.dot(m,n)*p1*dS, - ufl.dot(m, n)*p2*dS, None]]
L = [ufl.inner(f, v1) * dx(1), ufl.inner(f, v2) * dx(2), None, None, None]
a_cpp = dolfinx.fem.form(a)
L_cpp = dolfinx.fem.form(L)
# Lid velocity definition
def lid_velocity_expression(x):
return np.stack((np.ones(x.shape[1]), np.zeros(x.shape[1])))
lid_velocity = Function(V2)
lid_velocity.interpolate(lid_velocity_expression)
#definition of the boundary conditions
dofs_V1_down = dolfinx.fem.locate_dofs_topological(V1, boundaries.dim, facets_down_boundary)
dofs_V2_right = dolfinx.fem.locate_dofs_topological(V2, boundaries.dim, facets_up_right)
dofs_V2_left = dolfinx.fem.locate_dofs_topological(V2, boundaries.dim, facets_up_left)
dofs_V2_lid = dolfinx.fem.locate_dofs_topological(V2, boundaries.dim, facets_lid_boundary)
bc_down= dolfinx.fem.dirichletbc(zero, dofs_V1_down, V1)
bc_right= dolfinx.fem.dirichletbc(zero, dofs_V2_right, V2)
bc_left= dolfinx.fem.dirichletbc(zero, dofs_V2_left, V2)
bc_lid= dolfinx.fem.dirichletbc(lid_velocity, dofs_V2_lid, V2)
bcs= [bc_down, bc_right, bc_left, bc_lid]
#SOLVER
# Assemble the block linear system
A = multiphenicsx.fem.petsc.assemble_matrix_block(a_cpp, bcs=bcs, restriction=(restriction, restriction))
A.assemble()
F = multiphenicsx.fem.petsc.assemble_vector_block(L_cpp, a_cpp, bcs=bcs, restriction=restriction)
solv = multiphenicsx.fem.petsc.create_vector_block(L_cpp, restriction=restriction)
ksp = petsc4py.PETSc.KSP()
ksp.create(mesh.comm)
ksp.setOperators(A)
ksp.setType("preonly")
ksp.getPC().setType("lu")
ksp.getPC().setFactorSolverType("mumps")
ksp.setFromOptions()
ksp.solve(F, solv)
solv.ghostUpdate(addv=petsc4py.PETSc.InsertMode.INSERT, mode=petsc4py.PETSc.ScatterMode.FORWARD)
#SPLIT THE SOLUTIONS
# Split the block solution in components
(u_1, u_2, p_1, p_2, ll) = (dolfinx.fem.Function(V1), dolfinx.fem.Function(V2), dolfinx.fem.Function(Q1), dolfinx.fem.Function(Q2), dolfinx.fem.Function(M))
with multiphenicsx.fem.petsc.BlockVecSubVectorWrapper(
solv, [V1.dofmap, V2.dofmap, Q1.dofmap, Q2.dofmap, M.dofmap], restriction) as solv_wrapper:
for solv_wrapper_local, component in zip(solv_wrapper, (u_1, u_2, p_1, p_2, ll)):
with component.vector.localForm() as component_local:
component_local[:] = solv_wrapper_local
#SAVE THE SOLUTIONS
with XDMFFile(MPI.COMM_WORLD, "out_stokes/velocity1.xdmf", "w") as ufile_xdmf:
u_1.x.scatter_forward()
ufile_xdmf.write_mesh(mesh)
ufile_xdmf.write_function(u_1)
with XDMFFile(MPI.COMM_WORLD, "out_stokes/velocity2.xdmf", "w") as ufile_xdmf:
u_2.x.scatter_forward()
ufile_xdmf.write_mesh(mesh)
ufile_xdmf.write_function(u_2)
with XDMFFile(MPI.COMM_WORLD, "out_stokes/pressure1.xdmf", "w") as pfile_xdmf:
p_1.x.scatter_forward()
pfile_xdmf.write_mesh(mesh)
pfile_xdmf.write_function(p_1)
with XDMFFile(MPI.COMM_WORLD, "out_stokes/pressure2.xdmf", "w") as pfile_xdmf:
p_2.x.scatter_forward()
pfile_xdmf.write_mesh(mesh)
pfile_xdmf.write_function(p_2)