Strange behavior in deformation (Hyperelasticity)

1

Hi

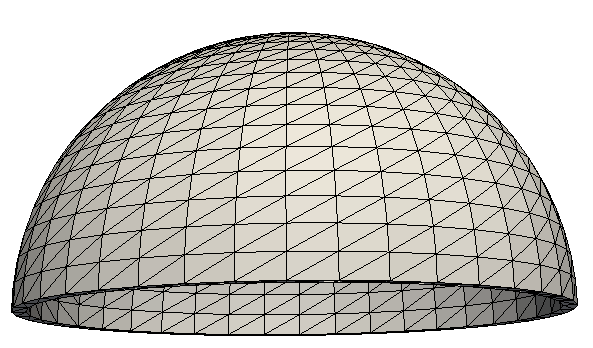
I have a 3D hyperelasticity problem. The domain is a hemisphere with radius 10 mm and thickness 0.5 mm as shown here:
A
The domain is fixed from the bottom and an internal pressure is applied on the internal surface. In strain energy term, I have an Ei function that I am approximating in the code. In addition I use numerical integration in a part of strain energy term.

The problem is that the deformation pattern changes when the pressure increases. For example when the internal pressure is 0.5 KPa the deformation is what I expect. When I increase it to 5 KPa, I expect the same deformation pattern but the deformation is completely different and the sphere swells hugely. Please look at this figure showing the deformed and undeformed states for 0.5 KPa and 5 KPa :

30
Increasing the quadrature degree or number of terms in function approximation or number of intervals in numerical integration were not helpful as I have already tried them.

Does anybody know why this strange behavior happens and might be resolved?

Here is the minimal work (I used GMSH to create the mesh):

from dolfin import *
import numpy as np

parameters["form_compiler"]["representation"] = "tsfc"

mesh = Mesh("mesh.xml")
x = SpatialCoordinate(mesh)

boundaries = MeshFunction("size_t", mesh, "mesh_facet_region.xml")
subdomains = MeshFunction("size_t", mesh, "mesh_physical_region.xml")

dx = Measure('dx', domain=mesh, subdomain_data=subdomains, metadata={'quadrature_degree': 2})
ds = Measure('ds', domain=mesh, subdomain_data=boundaries, metadata={'quadrature_degree': 2})

n = FacetNormal(mesh)

V = VectorFunctionSpace(mesh, 'Lagrange', degree=1)
u = Function(V)
v = TestFunction(V)

I = Identity(3)
F = I + grad(u)
C = F.T*F
Ic = tr(C)
J  = det(F)
Ic_bar = pow(J,-2./3.)*Ic

#Numerical Calculation of Integral using trapezoidal rule
def trapezoidal(f, a, b, n):

    h = (b - a) / n
    s = 0.0
    s += f(a)/2.0
    for i in range(1, n):
        s += f(a + i*h)
    s += f(b)/2.0
    return s * h

#Constants
a_1 = 100e3
a_3 = 5e3
a_4 = 500
K = 5
BULK = 1e7

# Ei function approximation
def Ei(X, k, b):

    LN = ln(X)

    for s in range(1, k + 1):
        fact = 1
        for i in range(1, s + 1):
            fact = fact * i
        b += (pow(-1., s + 1) * pow(-X, s) / (s * fact))

    return  LN - b

alpha =  atan(x[2]/x[0]) + np.pi/2

def G(theta):

    R = ((pow(cos(theta), 2) * C[0, 0] + pow(sin(theta), 2) * C[2, 2] )) ** (0.5)

    A_theta = 0.01 * exp(K * cos(2 * (theta - alpha)))

    F_R = a_3 * (exp(-a_4) * (Ei(a_4 * R, 50, 0) ) - ln(R) )

    return A_theta * F_R

G = trapezoidal(G, alpha - np.pi / 2., alpha + np.pi / 2., 10)

Pressure = Constant((5000.0))  # Deformation is completely different for Pressure = 500 and Pressure = 5000

psi = (a_1 * (Ic_bar - 3.) + G + 0.5 *  BULK * pow(ln(J),2)) * dx - inner(-Pressure * n, u) * ds(2)  # ds(2) corresponds to the inner surface of the sphere

F_total = derivative(psi, u, v)

bc = DirichletBC(V, Constant((0., 0., 0.)), boundaries, 1) # ds(1) corresponds to the bottom surface of the sphere (FIXED)

J1 = derivative(F_total, u)

problem = NonlinearVariationalProblem(F_total, u, bc, J1)
solver = NonlinearVariationalSolver(problem)
solver.solve()

File("Displacement.pvd") << u
2

Hi,
sorry but it is hard to help you since your problem seems only that the deformed shape is not what you expect. We don’t know what is expected, for instance the deformed shape for 0.5kPa is not so obvious to me, why the top surface goes down while it is subjected to internal pressure ? the deformed shape at 5 kPa makes more sense to me.
Do you have a quantitative measure with respect to a reference solution indicating that there is a problem ?
Did you try using a P2 interpolation for the displacement to see if you see some differences ?

3

Thanks for your response. The reason why the top of surface goes down is because of the term G in strain energy function. For example if I remove the G from the psi, the material behaves as nearly incompressible neo-Hokkean material and deformation pattern is similar to right figure I provides above (P = 5 KPa) for all pressure. But the term G takes care of fiber orientation in the material and the orientation is defined by alpha in the code. The way I have defined it above, by applying the internal pressure, the deformation is supposed to be : Swelling horizontally (NOT vertically) and top of the sphere goes down. Exactly like the left figure above. But I do not know why by increasing the pressure it goes up largely.
Regarding your suggestion to use P2 interpolation, I did a quick test and here is the results:

a3
a31085×365 200 KB

Again, the problem does not seem to be resolved.

4

But again, is there really a problem ? Do you have a reference solution to compare with at 5 kPa ?

5

Yes I do. You could find the reference here.
I was able to validate the model for a single element (Figure.4 in the reference) but I am having trouble with the figure.7. However I can reproduce the same deformation when the pressure is low (0.5KPa). The issue happens when I increase the pressure to 5KPa.