Velocity Field not working on Advection-Diffusion-Reaction

I/O
1

Hi everyone, I’m actually working on an ADR EDP solver using FeniCs, I’m pretty new at this library. In the FeniCs documentation I found an ADR EDP implementation example but it used a previous file with a velocity field solved from a Navier-Stokes problem.

In my code when I define the velocity field (that must depend on time) it seems to have no incidence in the solution, the behavior is like the advection term does not affect the problem, I’ll let my code in here,
(I changed the velocity field to a more exagerated one so i can be sure the field does not affect, the original one was: project(Expression((‘x[0]’+c,'x[1]’+c), degree=1),W))

from future import print_function

import matplotlib.pyplot as plt

from fenics import *

import numpy as np

T = 10.0 # final time

num_steps = 500 # number of time steps

dt = T / num_steps # time step size

eps = 0.001 # diffusion coefficient

bet = 10 # reaction rate

tht = 1

sig = 0.5

Create mesh

domain = Rectangle(Point(-1.0, -1.0), Point(1.0, 1.0))

mesh = generate_mesh(domain, 20)

Define function space for velocity

W = VectorFunctionSpace(mesh, ‘P’, 2)

Define function space for system of concentrations

P1 = FiniteElement(‘P’, triangle, 1)

element = MixedElement([P1, P1, P1])

V = FunctionSpace(mesh, element)

Define test functions

v_1, v_2, v_3 = TestFunctions(V)

Define functions for velocity and concentrations

w = Function(W)

u = Function(V)

u_0 = Expression((‘pow(x[0],2)+pow(x[1],2) > 0.01 ? 0.1 : 0’, ‘pow(x[0],2)+pow(x[1],2) < 0.01 ? 0.1 : 0’, ‘0’), degree=1)

u_n = project(u_0,V)

Split system functions to access components

u_1, u_2, u_3 = split(u)

u_n1, u_n2, u_n3 = split(u_n)

Define source terms

f_1 = Constant(0)

f_2 = Constant(0)

f_3 = Constant(0)

Define expressions used in variational forms

k = Constant(dt)

eps = Constant(eps)

bet = Constant(bet)

tht = Constant(tht)

sig = Constant(sig)

Define variational problem

F = ((u_1 - u_n1) / k)v_1dx + dot(w, grad(u_1))v_1dx \

  • epsdot(grad(u_1), grad(v_1))dx + betu_1u_2v_1dx \

  • ((u_2 - u_n2) / k)v_2dx + dot(w, grad(u_2))v_2dx \

  • epsdot(grad(u_2), grad(v_2))dx - betu_1u_2v_2dx + thtu_2v_2*dx \

  • ((u_3 - u_n3) / k)v_3dx + dot(w, grad(u_3))v_3dx \

  • epsdot(grad(u_3), grad(v_3))dx - sigu_2v_3*dx \

  • f_1v_1dx - f_2v_2dx - f_3v_3dx

Create VTK files for visualization output

vtkfile_u_1 = File(‘reaction_system/u_1.pvd’)

vtkfile_u_2 = File(‘reaction_system/u_2.pvd’)

vtkfile_u_3 = File(‘reaction_system/u_3.pvd’)

Time-stepping

t = 0

for n in range(num_steps):

Update current time

t += dt

Set velocity

##c = str(int(np.sin(np.pi*t)))

w = project(Expression((’-1’,’-1’), degree=1),W) #HERE IS THE PROBLEM

Solve variational problem for time step

solve(F == 0, u)

Save solution to file (VTK)

_u_1, _u_2, _u_3 = u.split()

vtkfile_u_1 << (_u_1, t)

vtkfile_u_2 << (_u_2, t)

vtkfile_u_3 << (_u_3, t)

Update previous solution

u_n.assign(u)

Hold plot

p = plot(_u_2)

plot(mesh)

plt.colorbar§

plt.show()

The solution looks like: 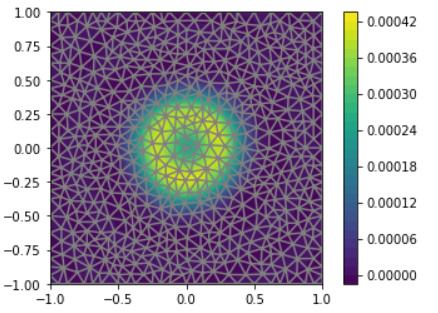Captura de pantalla (39)

I’m thinking that maybe I didn’t define well the velocity field since it was imported from a previous file in the example, as I’m not expert I don’t know and can’t find any problem like this in the web, hope you guys can help me, it is a really simple issue for sure!!

2

You are redefining w after the creation of the variational form. Move your definition of w

Or use w.assign(project(Expression((’-1’,’-1’), degree=1),W) ).

3

I have tried solving the same problem but in a simpler version. I tried use the method shown but I get this error message:

*** Error: Unable to define linear variational problem a(u, v) == L(v) for all v.
*** Reason: Expecting the left-hand side to be a bilinear form (not rank 1).
*** Where: This error was encountered inside LinearVariationalProblem.cpp.

Code:

P1 = FunctionSpace(mesh,‘Lagrange’,1)
W = VectorFunctionSpace(mesh,‘Lagrange’,2)

def boundary(x, on_boundary):
return on_boundary

bc = DirichletBC(V, Constant(0), boundary)

u = TrialFunction(P1)
v = TestFunction(P1)

w = Function(W)
u = Function(P1)
#w.assign(project(Expression((’-1’,’-1’), degree=1),W))
w = project(Expression((‘sin(x[0])’,‘sin(x[1])’), degree=1),W)

f = Constant(0) #

a = inner(grad(u), grad(v))dx + dot(w,grad(u))vdx
L = fv*dx

solve(a == L, u, bc)

4

Please format your code by using ``` encapsulation

5

Note that you are also redefining u before you define the variational form a.
I usually use u to define the trial function and uh to define the solution function.

1 Like