Any matrix generated by a DOLFINx form over a dx integral will have a specific preallocated sparsity pattern: https://github.com/FEniCS/dolfinx/blob/main/cpp/dolfinx/fem/sparsitybuild.cpp#L18-L31
which pre-allocates memory for potential non-zero entries for any dof sharing the same cell that the current DOF. This means that the matrix only has local entries, there are no nonlocal entries here (there might be off-diagonal ghost entries when running in parallel).
Without a minimal example where you illustrate how many non-zero entries you expect, and how many you get, it is hard to give any further guidance.
As the matrix returned by dolfinx is a PETSc matrix, you can use any PETsc option to modify the matrix options.
Here is a minimal code illustrating how you can split the DOLFINx code into several steps, inspecting what you send to the matrix creator:
import time
import dolfinx
import matplotlib.pyplot as plt
import numpy as np
import scipy.sparse
import ufl
from mpi4py import MPI
from petsc4py import PETSc
N = 10
degree = 2
mesh = dolfinx.mesh.create_unit_cube(MPI.COMM_WORLD, N, N, N)
V = dolfinx.fem.FunctionSpace(mesh, ("CG", degree))
u = ufl.TrialFunction(V)
v = ufl.TestFunction(V)
a = ufl.inner(u, v) * ufl.SpatialCoordinate(mesh)[1]**2 * ufl.dx
jit_parameters = {"cffi_extra_compile_args": ["-Ofast", "-march=native"],
"cffi_libraries": ["m"]}
form_a = dolfinx.fem.form(a, jit_params=jit_parameters)
sp = dolfinx.fem.create_sparsity_pattern(form_a)
sp.assemble()
print(f"Number of non-zeros in sparsity pattern: {sp.num_nonzeros}")
print(f"Num dofs: {V.dofmap.index_map.size_local * V.dofmap.index_map_bs}")
print(f"Entries per dof {sp.num_nonzeros/(V.dofmap.index_map.size_local * V.dofmap.index_map_bs)}")
print(f"Dofs per cell {V.element.space_dimension}")
print("-" * 25)
for option in [0, 1]:
A = dolfinx.cpp.la.petsc.create_matrix(mesh.comm, sp)
A.setOption(A.Option.IGNORE_ZERO_ENTRIES, option)
start = time.perf_counter()
dolfinx.fem.petsc.assemble_matrix(A, form_a)
A.assemble()
end = time.perf_counter()
print(f"PETSc ignore zero:{option} Assembly time: {end-start}")
b, c = A.createVecs()
start = time.perf_counter()
A.mult(c, b)
end = time.perf_counter()
print(f"PETSc ignore zero:{option} MatVec time: {end-start}")
print("-" * 25)
# Plot sparsity pattern
global_indices = np.asarray(V.dofmap.index_map.local_to_global(
np.arange(V.dofmap.index_map.size_local + V.dofmap.index_map.num_ghosts, dtype=np.int32)), dtype=PETSc.IntType)
sort_index = np.argsort(global_indices)
is_A = PETSc.IS().createGeneral(global_indices[sort_index])
A_loc = A.createSubMatrices(is_A)[0]
ai, aj, av = A_loc.getValuesCSR()
A_csr = scipy.sparse.csr_matrix((av, aj, ai))
plt.spy(A_csr)
plt.grid()
plt.savefig(f"local_sparsity_{option}_{MPI.COMM_WORLD.rank}.png")
A.destroy()
This returns the following pattern in serial:

and the following two in parallel
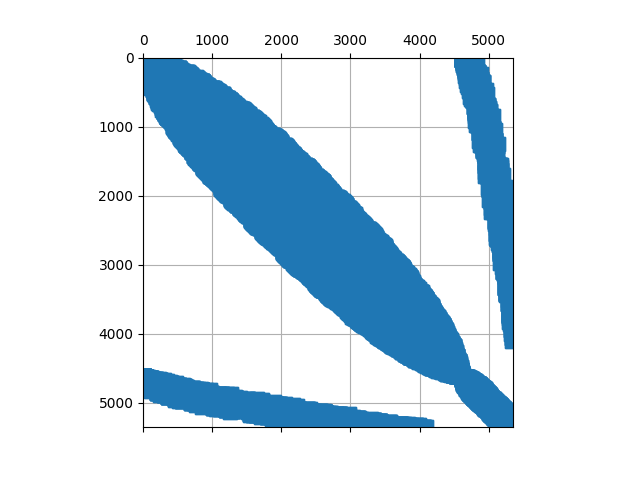

where the off diagonal entries are those on the process boundary that needs to be communciated.
I would also like to note that to speed up assemble, you can set the jit_parameters, as explained here.


