Starting from
in a one dimensional domain [0,1] where c_p and k are modeling two different materials:
I decided to refactor c_p to the right hand side such that
However, both solutions with FEniCS are different (this is a random time step, the trend is similar for all time steps):
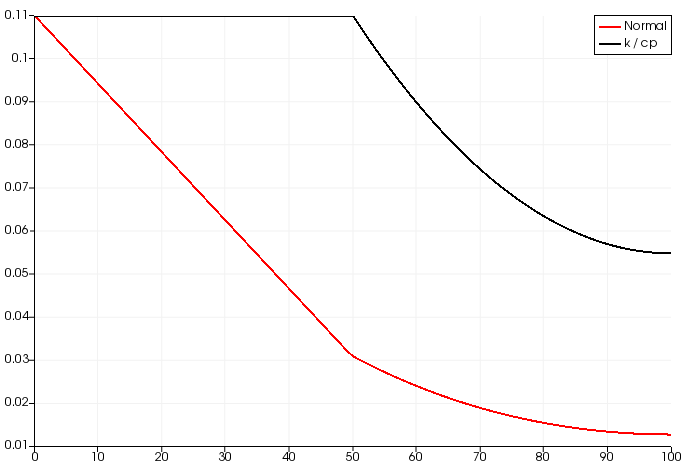
The one with c_p refactored shows a flat solution for x<0.5, whereas the original equation has a linear solution. This difference disappears when the material properties are homogeneous, which makes me think I might be committing some mistake in my finite element formulation. The code to run both examples is:
from fenics import *
cp_electrolyte = 1e-8
k_electrolyte = 1.0
k_electrode = 2.0
cp_electrode = 1.0
scan_rate = 1.0
output_dir = "./"
mesh = UnitIntervalMesh(100)
V = FunctionSpace(mesh, "CG", 1)
u, v = TrialFunction(V), TestFunction(V)
Vlimit = 1.0
tlimit = Vlimit / abs(scan_rate)
class Materials(UserExpression):
def __init__(self, electrode, electrolyte, **kwargs):
super().__init__(**kwargs) # This part is new!
self.electrolyte = electrolyte
self.electrode = electrode
def eval(self, values, x):
if x[0] < 0.5:
values[0] = self.electrolyte
else:
values[0] = self.electrode
k = Materials(k_electrode, k_electrolyte)
cp = Materials(cp_electrode, cp_electrolyte)
normal = False
def forward():
dt_value = 1e-2
dt = Constant(dt_value)
u_n = Function(V)
if normal:
a = cp * u / dt * v * dx + k * \
inner(Constant(1.0 / 2.0) * grad(u), grad(v)) * dx
L = (
cp * u_n / dt * v * dx
- k * inner(Constant(1.0 / 2.0) * grad(u_n), grad(v)) * dx
)
else:
a = u / dt * v * dx + k / cp * \
inner(Constant(1.0 / 2.0) * grad(u), grad(v)) * dx
L = (
u_n / dt * v * dx
- k / cp * inner(Constant(1.0 / 2.0) * grad(u_n), grad(v)) * dx
)
t = 0
T = tlimit * 5
n_steps = int(T / dt_value)
bcval = Expression("t", t=t, degree=1)
def Left(x, on_boundary):
return x[0] < DOLFIN_EPS and on_boundary
bc = DirichletBC(V, bcval, Left)
u_sol = Function(V)
if normal:
output = "potential.pvd"
else:
output = "potential_ratio.pvd"
potential_pvd = File(output)
while t < T:
solve(a == L, u_sol, bcs=bc)
t += dt_value
bcval.t = t
potential_pvd << u_sol
u_n.assign(u_sol)
return u_n
u_n = forward()
Thanks