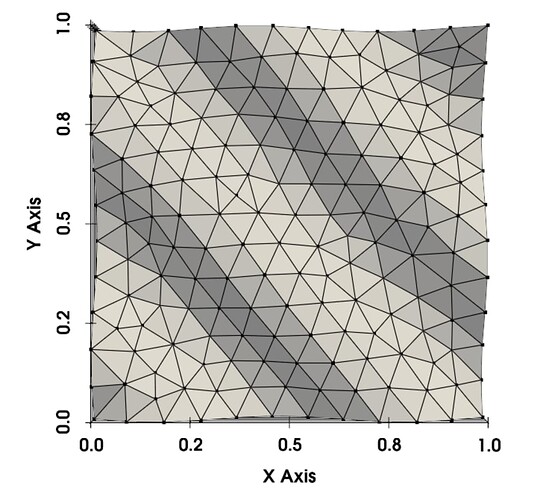
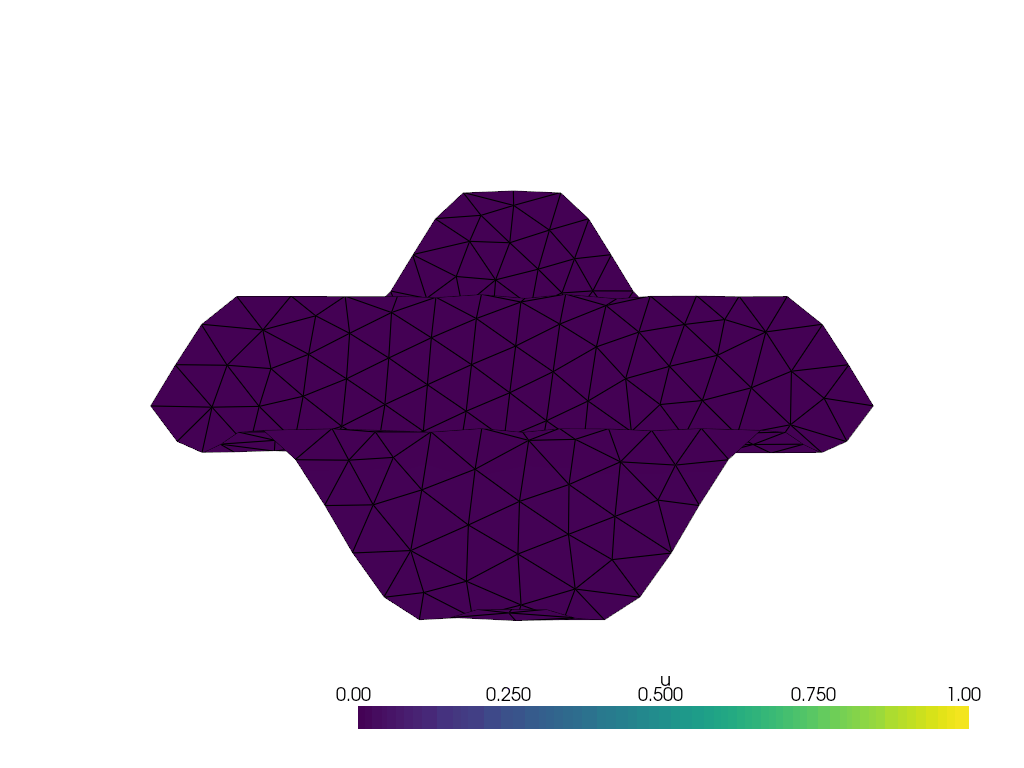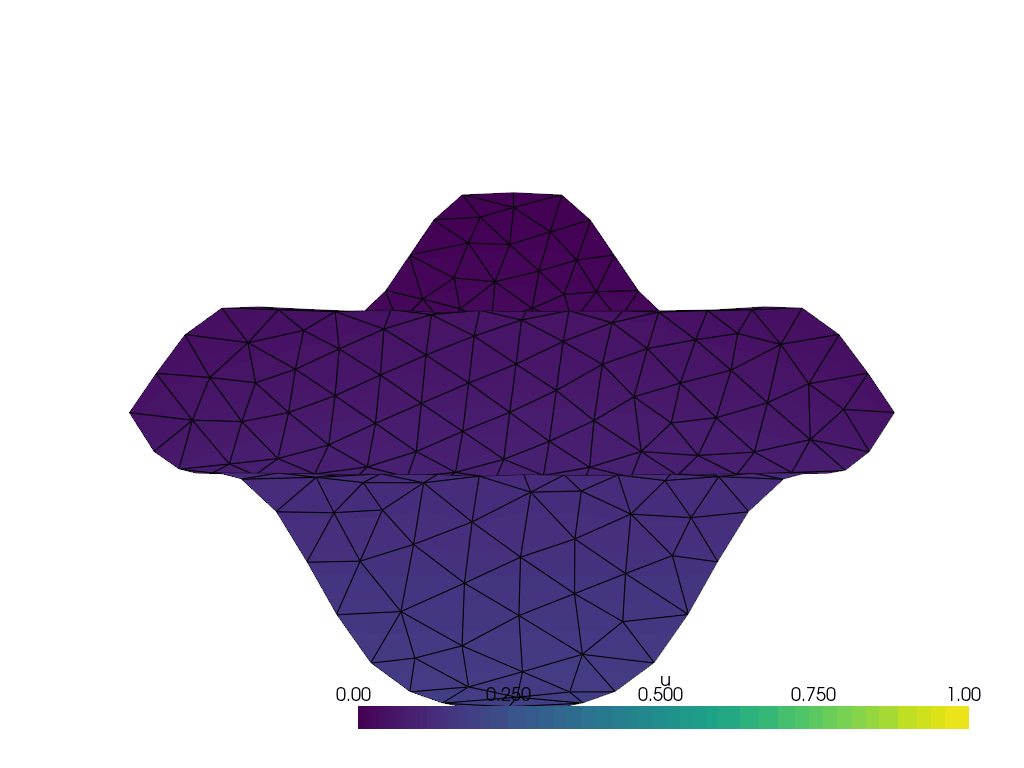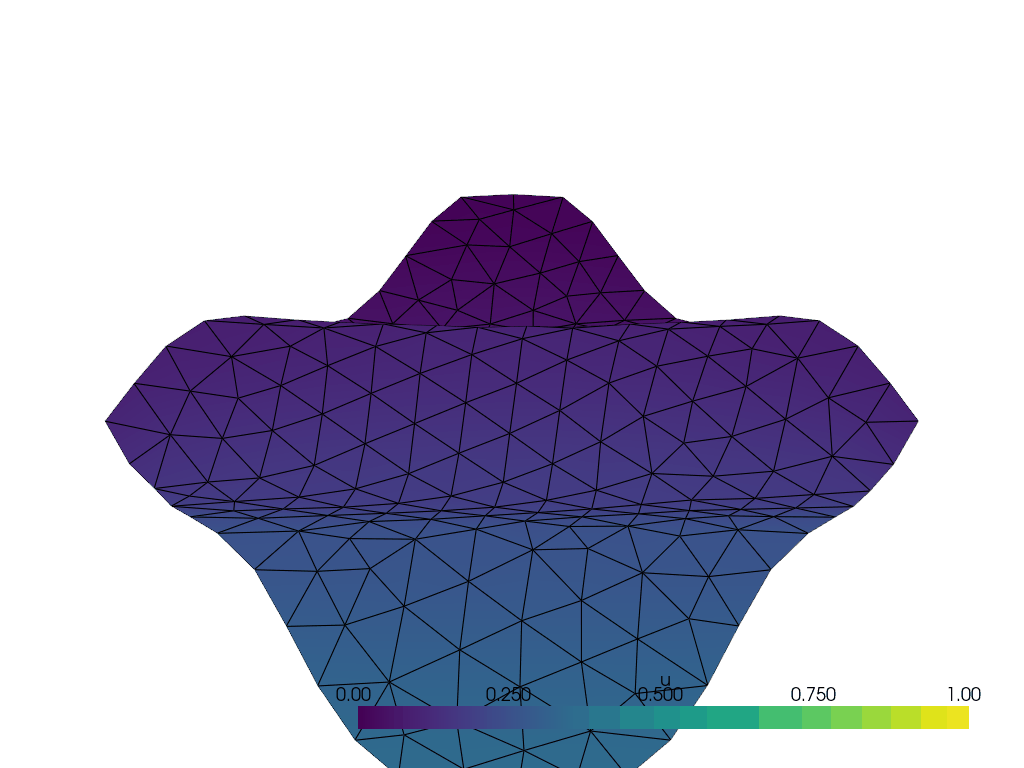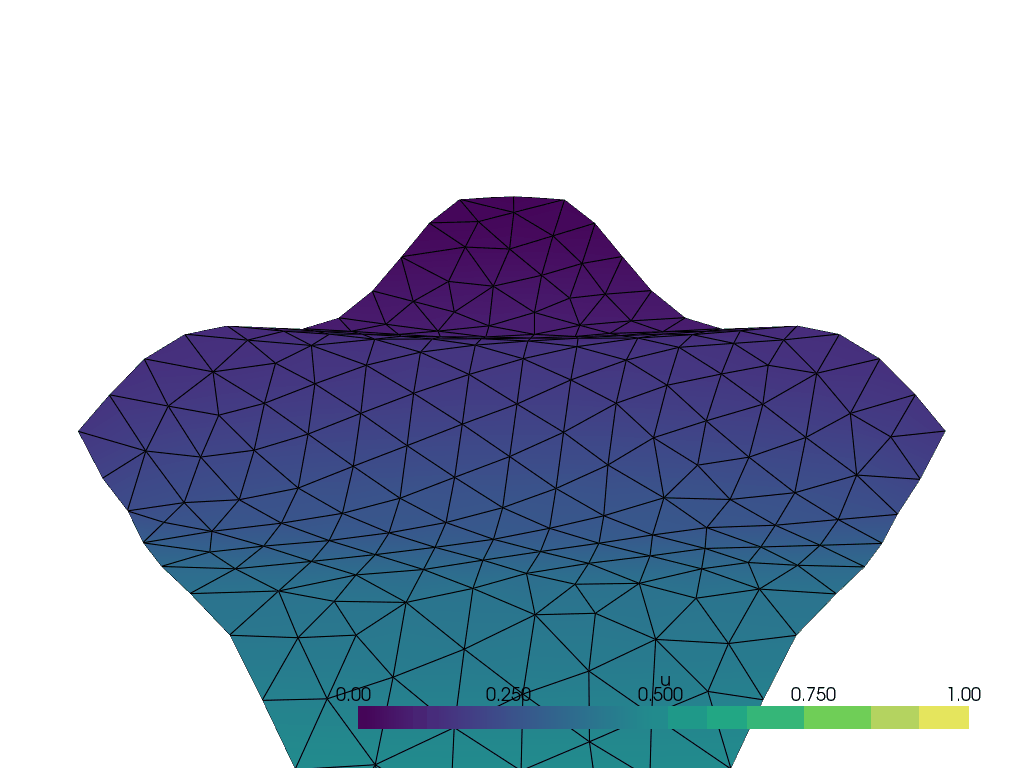
I have the following wavy 2D manifold defined by z = \frac{1}{10}\sin(10(x+y)) created with the following code with gmsh
## Identify vertices, cells, and tags for each vertex/node
gmsh.initialize()
gmsh.model.add("wavy plate")
coords = [] # The x, y, z coordinates of all the nodes
nodes = [] # The tags of the corresponding nodes
tris = [] # The connectivities of the triangle elements (3 node tags per triangle) on the plate w/ topography
lin = [[], [], [], []] # The connectivities of the line elements on the 4 boundaries (2 node tags for each line element)
pnt = [tag(0, 0), tag(N, 0), tag(N, N), tag(0, N)] # The connectivities of the point elements on the 4 corners (1 node tag for each point element)
for i in range(N + 1):
for j in range(N + 1):
nodes.append(tag(i, j))
coords.extend([
float(i) / N,
float(j) / N,
0.1 * np.sin(10 * float(i + j) / N)
])
if i > 0 and j > 0:
tris.extend([tag(i - 1, j - 1), tag(i, j - 1), tag(i - 1, j)])
tris.extend([tag(i, j - 1), tag(i, j), tag(i - 1, j)])
if (i == 0 or i == N) and j > 0:
lin[3 if i == 0 else 1].extend([tag(i, j - 1), tag(i, j)])
if (j == 0 or j == N) and i > 0:
lin[0 if j == 0 else 2].extend([tag(i - 1, j), tag(i, j)])
# Create 4 discrete points for the 4 corners of the terrain surface:
for i in range(4):
gmsh.model.addDiscreteEntity(dim = 0, tag = i + 1, boundary = []) # Create 4 corner points (dim = 0), with tags = {1,2,3,4}
# Set coordinates of each point (by tags = {1,2,3,4})
gmsh.model.setCoordinates(tag = 1,
x = 0,
y = 0,
z = coords[3 * tag(0, 0) - 1])
gmsh.model.setCoordinates(tag = 2,
x = coords[3 * tag(N, 0) - 1-2],
y = coords[3 * tag(N, 0) - 1-1],
z = coords[3 * tag(N, 0) - 1])
gmsh.model.setCoordinates(tag = 3,
x = coords[3 * tag(N, N) - 1-2],
y = coords[3 * tag(N, N) - 1-1],
z = coords[3 * tag(N, N) - 1])
gmsh.model.setCoordinates(tag = 4,
x = coords[3 * tag(0, N) - 1-2],
y = coords[3 * tag(0, N) - 1-1],
z = coords[3 * tag(0, N) - 1])
## Form Boundaries (by connecting 4 corner points)
for i in range(4): # 4 bounding curves
gmsh.model.addDiscreteEntity(dim = 1, tag = i + 1, boundary = [i + 1, i + 2 if i < 3 else 1])# Creates 4 discrete bounding curves, with their boundary points
# Define (skeleton of) the surface
surface = gmsh.model.add_discrete_entity(dim = 2, tag = 1, boundary = [1,2,-3,-4]) # So far, surface just the 4 corners
## Add the nodes, points, lines, and cells to the surface
gmsh.model.mesh.addNodes(2, 1, nodes, coords) # Add nodes to surface
for i in range(4):
# Type 15 for point elements:
gmsh.model.mesh.addElementsByType(i + 1, 15, [], [pnt[i]]) # Add points to surface
# Type 1 for 2-node line elements:
gmsh.model.mesh.addElementsByType(i + 1, 1, [], lin[i]) # Add lines to surface
gmsh.model.mesh.addElementsByType(1, 2, [], tris) # Add elements/cells to surface (type 2 for 3-node triangular elements)
gmsh.model.mesh.reclassifyNodes() # Reclassify the nodes on the curves and the points
gmsh.model.mesh.createGeometry() # Create a geometry for the discrete curves and surfaces
gmsh.model.occ.synchronize() # Probably a good idea to synchronize before generating mesh
## Add Physical Group (important step for Dolfinx meshing)
areas = gmsh.model.getEntities(dim=2)
fluid_marker = 11 # What do you want the fluid marker to be named?
gmsh.model.addPhysicalGroup(areas[0][0], [areas[0][1]], fluid_marker) # Create the physical group
gmsh.model.setPhysicalName(areas[0][0], fluid_marker, "Fluid area")
## Mesh refinement
res = 1/10
gmsh.option.setNumber("Mesh.CharacteristicLengthMin", res)
gmsh.option.setNumber("Mesh.CharacteristicLengthMax", res)
## Generate mesh
gmsh.model.occ.synchronize()
gmsh.model.mesh.generate(2)
model_rank = 0
mesh, cell_tags, facet_tags = df.io.gmshio.model_to_mesh(gmsh.model, MPI.COMM_WORLD, model_rank)
I want to solve Poisson’s Equation, -\Delta u = f, on this manifold with Dirichlet boundary conditions. The variational form for Poisson’s Equation should still be
\int_\Omega \nabla u \cdot \nabla v d\Omega= \int_\Omega fv d\Omega
and for this to work, ufl.grad() needs to “understand” that the mesh is a wavy 2D manifold, not a flat x-y plane.
If it does not understand the context of the geometry of the mesh that the problem is being solved on, how would a problem like this be handled?