Ncurl elements and DG0 material properties

dolfinx
1

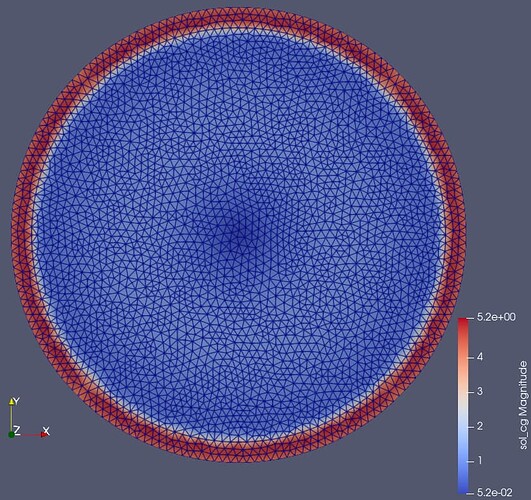
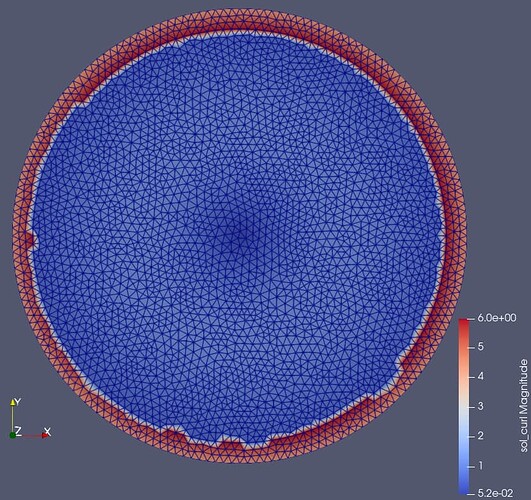
I’m using DG0 elements to assign materials to mesh regions like in this example. When I use these material DG0 functions together with Ncurl elements I get ragged field on the material boundary like in the picture below (compared to the vector CG elements). When using this function in further calculations errors pile up resulting in unstable solution and wrong results.

What can I do to fix this behaviour?

PS. I didn’t experience this behaviour in Dolfin

CG Ncurl
cg
cg829×780 118 KB
curl
curl830×781 115 KB

Gmsh model mesh.geo:

Geometry.OCCTargetUnit = "M";

r1 = 1;
r2 = 1.1;
dx1 = 0.5;
dy1 = 0.5;
dx2 = 0.5;
dy2 = 0.5;
mesh1 = 0.04;
mesh2 = 0.04;

p0 = newp; Point(p0) = {dx1,dy1,0,mesh1};
p1 = newp; Point(p1) = {r1+dx1,dy1,0,mesh1};
p2 = newp; Point(p2) = {dx1,r1+dy1,0,mesh1};
p3 = newp; Point(p3) = {-r1+dx1,dy1,0,mesh1};
p4 = newp; Point(p4) = {dx1,-r1+dy1,0,mesh1};
l1 = newl; Circle(l1) = {p1,p0,p2};
l2 = newl; Circle(l2) = {p2,p0,p3};
l3 = newl; Circle(l3) = {p3,p0,p4};
l4 = newl; Circle(l4) = {p4,p0,p1};
ll1 = newll; Line loop(ll1) = {l1,l2,l3,l4};
s1 = news; Surface(s1) = {ll1};

p00 = newp; Point(p00) = {dx2,dy2,0,mesh2};
p10 = newp; Point(p10) = {r2+dx2,dy2,0,mesh2};
p20 = newp; Point(p20) = {dx2,r2+dy2,0,mesh2};
p30 = newp; Point(p30) = {-r2+dx2,dy2,0,mesh2};
p40 = newp; Point(p40) = {dx2,-r2+dy2,0,mesh2};
l10 = newl; Circle(l10) = {p10,p00,p20};
l20 = newl; Circle(l20) = {p20,p00,p30};
l30 = newl; Circle(l30) = {p30,p00,p40};
l40 = newl; Circle(l40) = {p40,p00,p10};
ll10 = newll; Line loop(ll10) = {l10,l20,l30,l40};
s10 = news; Surface(s10) = {ll10, ll1};

Physical Surface(1) = {s1};
Physical Surface(2) = {s10};

Generate gmsh mesh mesh.msh using command gmsh mesh.geo -2

DolfinX code:

import dolfinx
import dolfinx.io
import ufl
import numpy as np
from mpi4py import MPI


def convert_msh(input_file: str, output_file: str,
                cell_type="triangle", cell_data_tag="gmsh:physical"):
    import meshio

    msh = meshio.read(input_file)
    msh.prune_z_0()
    msh.remove_orphaned_nodes()
    cells = msh.get_cells_type(cell_type)
    regions = msh.get_cell_data(cell_data_tag, cell_type)
    out_mesh = meshio.Mesh(points=msh.points,
                           cells={cell_type: cells},
                           cell_data={"regions": [regions]})
    meshio.write(output_file, out_mesh, file_format="xdmf")

# convert mesh to dolfinx
convert_msh("mesh.msh", "mesh.xdmf")

with dolfinx.io.XDMFFile(MPI.COMM_WORLD, "mesh.xdmf", "r") as xdmf:
    mesh = xdmf.read_mesh(name="Grid")
    subdomains = xdmf.read_meshtags(mesh, name="Grid")

# assign material
V = dolfinx.FunctionSpace(mesh, ("Discontinuous Lagrange", 0))
mat = dolfinx.Function(V)
mat.name = "material"
with mat.vector.localForm() as loc:
    loc.set(0)
    cells = subdomains.indices[subdomains.values == 2]
    loc.setValues(cells, np.full(cells.size, 1))

H1 = ufl.FiniteElement("Lagrange", mesh.ufl_cell(), 2)
Hvec = ufl.VectorElement(H1, dim=2)
Hcurl = ufl.FiniteElement("Nedelec 1st kind H(curl)", mesh.ufl_cell(), 2)

# source function
V = dolfinx.FunctionSpace(mesh, H1)
f = dolfinx.Function(V)
f.name = "source"
f.interpolate(lambda x: np.exp(- (x[0] - 0.5)**2 / (2 * 0.5**2)
                          - (x[1] - 0.5)**2 / (2 * 0.5**2)))

# CG solution
V = dolfinx.FunctionSpace(mesh, Hvec)
sol_cg = dolfinx.Function(V)
sol_cg.name = "sol_cg"
u, v = ufl.TrialFunction(V), ufl.TestFunction(V)
a = ufl.inner(u, v) * ufl.dx
L = ufl.inner(ufl.grad(f) + 10 * mat * ufl.grad(f), v) * ufl.dx
dolfinx.fem.LinearProblem(a, L, u=sol_cg).solve()

# Hcurl solution
V = dolfinx.FunctionSpace(mesh, Hcurl)
sol_curl = dolfinx.Function(V)
sol_curl.name = "sol_curl"
u, v = ufl.TrialFunction(V), ufl.TestFunction(V)
a = ufl.inner(u, v) * ufl.dx
L = ufl.inner(ufl.grad(f) + 10 * mat * ufl.grad(f), v) * ufl.dx
dolfinx.fem.LinearProblem(a, L, u=sol_curl).solve()

with dolfinx.io.XDMFFile(MPI.COMM_WORLD, "out.xdmf", "w") as xdmf:
    xdmf.write_mesh(mesh)
    xdmf.write_function(mat)
    xdmf.write_function(f)
    xdmf.write_function(sol_cg)
    xdmf.write_function(sol_curl)
2

One thing you need to consider is if this is behavior due to the visualization (as the dolfinx xdmf format saves data as CG-1, if it is not DG-0, while dolfin’s XDMF.write_checkpoint saves arbitrary order CG/DG fields).

You could for instance use pyvista to test this, as shown in: dolfinx/demo_pyvista.py at main · FEniCS/dolfinx · GitHub

There is also an open pull request adding support for ADIOS2VTX, Which can do arbitrary order VG/DG with newer releases of paraview( see: ADIOS2 support (VTX and Fides) by jorgensd · Pull Request #1655 · FEniCS/dolfinx · GitHub for details)

1 Like
3

I think you’re right. Projecting Hcrul result onto the vector CG yielded the same result.

But I’ve noticed that the boundary artefacts, visible on the Hcurl solution are present on the CG, they are just not so obvious (green circles in pictures below).

CG Ncurl
H1
H1906×811 168 KB
Hcurl
Hcurl910×800 164 KB
4

Nedelec 1st kind span the space (DefElement: Nédélec (first kind))
by:

image
image1183×749 122 KB

while Lagrange span:
image
image1466×535 77.5 KB

In particular, the tangential components of h-curl are discontinuous, which is not captured by paraview (xdmf format in dolfin-x).

In the previous post I explained how to visualize higher order DG, and I would suggest you project your h1-curl solution into a higher order DG space and visualize it with either of the suggested approaches:

2 Likes
5

If anyone has a similar issue.
It’s better to pay more attention to the mesh generation to avoid such issues. Gmsh’s transfinite curves allow creating uniform meshes in such regions.

Transfinite Curve{l1,l2,l3,l4} = 50;
Transfinite Curve{l10,l20,l30,l40} = 50;