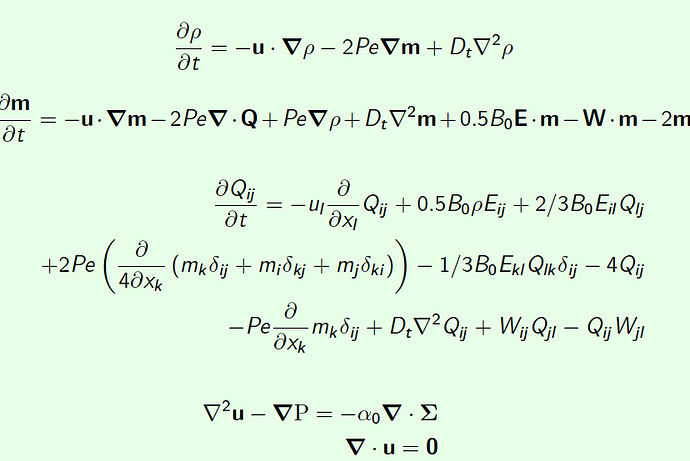Hello,
Is there a simple way to parallelize the heat equation tutorial (Diffusion of a Gaussian function — FEniCSx tutorial) ?
I am new to parallelization and I am wondering if the solver used in the tutorial is capable of supporting it.
solver = PETSc.KSP().create(domain.comm)
solver.setOperators(A)
solver.setType(PETSc.KSP.Type.PREONLY)
solver.getPC().setType(PETSc.PC.Type.LU)
Thank you.
What do you mean by parallelizing it?
The code runs fine in parallel (as this is done on the CI: fix runs-on · jorgensd/dolfinx-tutorial@40cae40 · GitHub)
All codes from the tutorial can be executed in parallel with mpirun -n 2 python3 name_of_script.py
Yes, by parallel I meant running the code in parallel with mpirun.
I am able to execute the code using the command mpirun -n 2 python3 name_of_script.py but when I try to increase the number of processes to 3 or more, it doesn’t work anymore. Am I missing something obvious?
What do you mean by it doesn’t work.
Does it throw an error?
Does it hang, if so where does it hang?
Here is an example of me running the heat code:
root@dokken-XPS-9320:~/shared# mpirun -n 2 python3 heat_code.py
L2-error: 2.83e-02
Error_max: 3.55e-15
root@dokken-XPS-9320:~/shared# mpirun -n 3 python3 heat_code.py
L2-error: 2.83e-02
Error_max: 2.66e-15
root@dokken-XPS-9320:~/shared# mpirun -n 5 python3 heat_code.py
L2-error: 2.83e-02
Error_max: 3.55e-15
using docker run -ti --network=host -v $(pwd):/root/shared -w /root/shared --rm ghcr.io/fenics/dolfinx/dolfinx:v0.6.0-r1
Can you provide the error message? Maybe it is realted not to the fenics code but to mpi itself.
Try running mpirun --use-hwthread-cpus python3 file.py, this (I think) will allow your computer to use all available cores. It is better explained here.
Hello, I apologize for the inconvenience, but I have checked and the heat equation tutorial works correctly in parallel on my computer. The problem arises from the fact that in the code I used, I added a few extra lines to solve another PDE on a submesh of the parent mesh.
I defined my submesh as follows:
submesh, entity_map, _, _ = dolfinx.mesh.create_submesh(mesh, mesh.topology.dim, cell_tags.indices[(cell_tags.values==1)])
Does the create_submesh function work in parallel now, or would it be better to use MeshView as indicated in this post Use of Submesh in parallel - #2 by dokken ? In that case, I don’t understand how my code could work for 2 processes and not more.
Thank you in advance.
Submesh works in parallel. Could you please add whatever extra lines you are adding to your code (so that we have a reproducible example to use for debugging).
Thank you very much for your response. Here is a shortened version of the code that I’m using:
#!/usr/bin/env python
# coding: utf-8
# Global objective: solve advection-diffusion equation
import numpy as np
import io
from mpi4py import MPI
import ufl
from ufl import Measure, FacetNormal
import matplotlib.pyplot as plt
import dolfinx
from dolfinx import fem, plot
from dolfinx.io import XDMFFile
from dolfinx.fem import FunctionSpace, VectorFunctionSpace, Constant, Function
from dolfinx.plot import create_vtk_mesh
from petsc4py import PETSc
from petsc4py.PETSc import ScalarType
# Read the mesh
with XDMFFile(MPI.COMM_WORLD, "mesh.xdmf", "r") as xdmf:
mesh = xdmf.read_mesh(name="Grid")
cell_tags = xdmf.read_meshtags(mesh, name="Grid")
mesh.topology.create_connectivity(mesh.topology.dim-1, mesh.topology.dim)
with XDMFFile(MPI.COMM_WORLD, "facet_mesh.xdmf", "r") as xdmf:
facet_tags = xdmf.read_meshtags(mesh, name="Grid")
# PART 1: solve fluid flow at steady state on submesh
# create submesh to solve flow problem
submesh, entity_map, _, _ = dolfinx.mesh.create_submesh(mesh, mesh.topology.dim, cell_tags.indices[(cell_tags.values==106)|(cell_tags.values==107)])
# method to transfer facet tags from parent mesh to submesh
# taken from: https://fenicsproject.discourse.group/t/problem-transferring-facet-tags-to-submesh/11213
tdim = mesh.topology.dim
fdim = tdim - 1
c_to_f = mesh.topology.connectivity(tdim, fdim)
f_map = mesh.topology.index_map(fdim)
all_facets = f_map.size_local + f_map.num_ghosts
all_values = np.zeros(all_facets, dtype=np.int32)
all_values[facet_tags.indices] = facet_tags.values
submesh.topology.create_entities(fdim)
subf_map = submesh.topology.index_map(fdim)
submesh.topology.create_connectivity(tdim, fdim)
c_to_f_sub = submesh.topology.connectivity(tdim, fdim)
num_sub_facets = subf_map.size_local + subf_map.size_global
sub_values = np.empty(num_sub_facets, dtype=np.int32)
for i, entity in enumerate(entity_map):
parent_facets = c_to_f.links(entity)
child_facets = c_to_f_sub.links(i)
for child, parent in zip(child_facets, parent_facets):
sub_values[child] = all_values[parent]
sub_meshtag = dolfinx.mesh.meshtags(submesh, submesh.topology.dim-1, np.arange(
num_sub_facets, dtype=np.int32), sub_values)
# Finite element function space for pressure
U = FunctionSpace(submesh, ("CG", 2))
# Trial and test functions
p, u = ufl.TrialFunction(U), ufl.TestFunction(U)
# Boundary conditions
# Dirichlet: p=0 on side 2
boundary_dofs = fem.locate_dofs_topological(U, submesh.topology.dim-1, sub_meshtag.indices[sub_meshtag.values == 2])
bc_inj = fem.dirichletbc(ScalarType(0), boundary_dofs, U)
bc_tot = [bc_inj]
The mesh can be accessed through the following link:
This code is quite lengthy and complex. Could you try to simplify it? (As I don’t have bandwidth to debug this whole code for you).
Yes, of course, I modified the code directly on my previous post to show only the beginning part where the facet tags of the parent mesh are projected onto those of the submesh because, after debugging, I realized that this part is already not working.
When I run the command mpirun -np 8 python3 test.py , I get the following error message:
python3: /src/dolfinx/cpp/dolfinx/graph/AdjacencyList.h:101: int dolfinx::graph::AdjacencyList<T>::num_links(int) const [with T = int]: Assertion `(node + 1) < (int)_offsets.size()' failed.
Loguru caught a signal: SIGABRT
python3: /src/dolfinx/cpp/dolfinx/graph/AdjacencyList.h:101: int dolfinx::graph::AdjacencyList<T>::num_links(int) const [with T = int]: Assertion `(node + 1) < (int)_offsets.size()' failed.
Loguru caught a signal: SIGABRT
python3: /src/dolfinx/cpp/dolfinx/graph/AdjacencyList.h:101: int dolfinx::graph::AdjacencyList<T>::num_links(int) const [with T = int]: Assertion `(node + 1) < (int)_offsets.size()' failed.
Loguru caught a signal: SIGABRT
Stack trace:
26 0x564062e57ab5 _start + 37
25 0x7fa90e52ae40 __libc_start_main + 128
24 0x7fa90e52ad90 /lib/x86_64-linux-gnu/libc.so.6(+0x29d90) [0x7fa90e52ad90]
23 0x564062e57bbd Py_BytesMain + 45
22 0x564062e81b7e Py_RunMain + 702
21 0x564062e90673 _PyRun_AnyFileObject + 67
20 0x564062e90978 _PyRun_SimpleFileObject + 424
19 0x564062e91495 python3(+0x264495) [0x564062e91495]
18 0x564062e8a55b python3(+0x25d55b) [0x564062e8a55b]
17 0x564062e91748 python3(+0x264748) [0x564062e91748]
16 0x564062e64cb6 PyEval_EvalCode + 134
15 0x564062d6ede6 python3(+0x141de6) [0x564062d6ede6]
14 0x564062d78152 _PyEval_EvalFrameDefault + 24994
13 0x564062d89b6c _PyFunction_Vectorcall + 124
12 0x564062d78a81 _PyEval_EvalFrameDefault + 27345
11 0x564062d7fe4b _PyObject_MakeTpCall + 603
10 0x564062d8931e python3(+0x15c31e) [0x564062d8931e]
9 0x7fa902197b50 /usr/local/dolfinx-real/lib/python3.10/dist-packages/dolfinx/cpp.cpython-310-x86_64-linux-gnu.so(+0x79b50) [0x7fa902197b50]
8 0x7fa902209f31 /usr/local/dolfinx-real/lib/python3.10/dist-packages/dolfinx/cpp.cpython-310-x86_64-linux-gnu.so(+0xebf31) [0x7fa902209f31]
7 0x7fa901f82b62 dolfinx::fem::locate_dofs_topological(dolfinx::fem::FunctionSpace const&, int, std::span<int const, 18446744073709551615ul>, bool) + 722
6 0x7fa901f81a0e /usr/local/dolfinx-real/lib/libdolfinx.so.0.6(+0xa8a0e) [0x7fa901f81a0e]
5 0x7fa90e53ae96 /lib/x86_64-linux-gnu/libc.so.6(+0x39e96) [0x7fa90e53ae96]
4 0x7fa90e52971b /lib/x86_64-linux-gnu/libc.so.6(+0x2871b) [0x7fa90e52971b]
3 0x7fa90e5297f3 abort + 211
2 0x7fa90e543476 raise + 22
1 0x7fa90e597a7c pthread_kill + 300
0 0x7fa90e543520 /lib/x86_64-linux-gnu/libc.so.6(+0x42520) [0x7fa90e543520]
2023-05-25 09:00:50.886 ( 0.752s) [main ] :0 FATL| Signal: SIGABRT
Stack trace:
26 0x5616b67e1ab5 _start + 37
25 0x7f5bc5c75e40 __libc_start_main + 128
24 0x7f5bc5c75d90 /lib/x86_64-linux-gnu/libc.so.6(+0x29d90) [0x7f5bc5c75d90]
23 0x5616b67e1bbd Py_BytesMain + 45
22 0x5616b680bb7e Py_RunMain + 702
21 0x5616b681a673 _PyRun_AnyFileObject + 67
20 0x5616b681a978 _PyRun_SimpleFileObject + 424
19 0x5616b681b495 python3(+0x264495) [0x5616b681b495]
18 0x5616b681455b python3(+0x25d55b) [0x5616b681455b]
17 0x5616b681b748 python3(+0x264748) [0x5616b681b748]
16 0x5616b67eecb6 PyEval_EvalCode + 134
15 0x5616b66f8de6 python3(+0x141de6) [0x5616b66f8de6]
14 0x5616b6702152 _PyEval_EvalFrameDefault + 24994
13 0x5616b6713b6c _PyFunction_Vectorcall + 124
12 0x5616b6702a81 _PyEval_EvalFrameDefault + 27345
11 0x5616b6709e4b _PyObject_MakeTpCall + 603
10 0x5616b671331e python3(+0x15c31e) [0x5616b671331e]
9 0x7f5bb9897b50 /usr/local/dolfinx-real/lib/python3.10/dist-packages/dolfinx/cpp.cpython-310-x86_64-linux-gnu.so(+0x79b50) [0x7f5bb9897b50]
8 0x7f5bb9909f31 /usr/local/dolfinx-real/lib/python3.10/dist-packages/dolfinx/cpp.cpython-310-x86_64-linux-gnu.so(+0xebf31) [0x7f5bb9909f31]
7 0x7f5bb9682b62 dolfinx::fem::locate_dofs_topological(dolfinx::fem::FunctionSpace const&, int, std::span<int const, 18446744073709551615ul>, bool) + 722
6 0x7f5bb9681a0e /usr/local/dolfinx-real/lib/libdolfinx.so.0.6(+0xa8a0e) [0x7f5bb9681a0e]
5 0x7f5bc5c85e96 /lib/x86_64-linux-gnu/libc.so.6(+0x39e96) [0x7f5bc5c85e96]
4 0x7f5bc5c7471b /lib/x86_64-linux-gnu/libc.so.6(+0x2871b) [0x7f5bc5c7471b]
3 0x7f5bc5c747f3 abort + 211
2 0x7f5bc5c8e476 raise + 22
1 0x7f5bc5ce2a7c pthread_kill + 300
0 0x7f5bc5c8e520 /lib/x86_64-linux-gnu/libc.so.6(+0x42520) [0x7f5bc5c8e520]
2023-05-25 09:00:50.886 ( 0.769s) [main ] :0 FATL| Signal: SIGABRT
Stack trace:
26 0x55d7befb1ab5 _start + 37
25 0x7fc35f973e40 __libc_start_main + 128
24 0x7fc35f973d90 /lib/x86_64-linux-gnu/libc.so.6(+0x29d90) [0x7fc35f973d90]
23 0x55d7befb1bbd Py_BytesMain + 45
22 0x55d7befdbb7e Py_RunMain + 702
21 0x55d7befea673 _PyRun_AnyFileObject + 67
20 0x55d7befea978 _PyRun_SimpleFileObject + 424
19 0x55d7befeb495 python3(+0x264495) [0x55d7befeb495]
18 0x55d7befe455b python3(+0x25d55b) [0x55d7befe455b]
17 0x55d7befeb748 python3(+0x264748) [0x55d7befeb748]
16 0x55d7befbecb6 PyEval_EvalCode + 134
15 0x55d7beec8de6 python3(+0x141de6) [0x55d7beec8de6]
14 0x55d7beed2152 _PyEval_EvalFrameDefault + 24994
13 0x55d7beee3b6c _PyFunction_Vectorcall + 124
12 0x55d7beed2a81 _PyEval_EvalFrameDefault + 27345
11 0x55d7beed9e4b _PyObject_MakeTpCall + 603
10 0x55d7beee331e python3(+0x15c31e) [0x55d7beee331e]
9 0x7fc353597b50 /usr/local/dolfinx-real/lib/python3.10/dist-packages/dolfinx/cpp.cpython-310-x86_64-linux-gnu.so(+0x79b50) [0x7fc353597b50]
8 0x7fc353609f31 /usr/local/dolfinx-real/lib/python3.10/dist-packages/dolfinx/cpp.cpython-310-x86_64-linux-gnu.so(+0xebf31) [0x7fc353609f31]
7 0x7fc353382b62 dolfinx::fem::locate_dofs_topological(dolfinx::fem::FunctionSpace const&, int, std::span<int const, 18446744073709551615ul>, bool) + 722
6 0x7fc353381a0e /usr/local/dolfinx-real/lib/libdolfinx.so.0.6(+0xa8a0e) [0x7fc353381a0e]
5 0x7fc35f983e96 /lib/x86_64-linux-gnu/libc.so.6(+0x39e96) [0x7fc35f983e96]
4 0x7fc35f97271b /lib/x86_64-linux-gnu/libc.so.6(+0x2871b) [0x7fc35f97271b]
3 0x7fc35f9727f3 abort + 211
2 0x7fc35f98c476 raise + 22
1 0x7fc35f9e0a7c pthread_kill + 300
0 0x7fc35f98c520 /lib/x86_64-linux-gnu/libc.so.6(+0x42520) [0x7fc35f98c520]
2023-05-25 09:00:50.887 ( 0.630s) [main ] :0 FATL| Signal: SIGABRT
===================================================================================
= BAD TERMINATION OF ONE OF YOUR APPLICATION PROCESSES
= PID 6228 RUNNING AT b6ebe4aa250a
= EXIT CODE: 134
= CLEANING UP REMAINING PROCESSES
= YOU CAN IGNORE THE BELOW CLEANUP MESSAGES
===================================================================================
YOUR APPLICATION TERMINATED WITH THE EXIT STRING: Aborted (signal 6)
This typically refers to a problem with your application.
Please see the FAQ page for debugging suggestions
Hi, im try to parallelize a code that solves this system, but when I run in paralell with 3 cpu the solution take a lot of time, im using like 60 thousand nodes. My system is a 2D system solving a system of 7 variables (scalar, vector and tensor advection-diffusion transient equations)-coupled with stokes equation on a circular domain. which strategy i could use to acelerate the solvers? and also it is psoible usign parallel simulation on fenicsx save the data in vtk to visualize when the code is ruining? (I found that only works on xdmf format (on parallel), but only is posible to ploting when the run is over). can you please give some advise?
First of all, how many degrees of freedom are there in the total system?
Secondly, what kind of solver are you using?
If you want to plot during simulation, I would suggest using @Stein’s pyvista4dolfinx: Pyvista4dolfinx
Hi, thanks for reply.
This is my system of equations :
density (rho)
\begin{equation*}
\frac{\partial \rho}{\partial t} = -\mathbf{u}\cdot\boldsymbol{\nabla}\rho -2Pe\boldsymbol{\nabla}\mathbf{m} + D_{t}\nabla^{2}\rho
\end{equation*}
polarization vector m
\begin{equation*}
\frac{\partial \mathbf{m}}{\partial t} = -\mathbf{u}\cdot\boldsymbol{\nabla}\mathbf{m} -2Pe\boldsymbol{\nabla}\cdot\mathbf{Q} + Pe\boldsymbol{\nabla}\rho + D_{t}\nabla^{2}\mathbf{m} + 0.5B_{0}\mathbf{E}\cdot\mathbf{m} - \mathbf{W}\cdot\mathbf{m} - 2\mathbf{m}
\end{equation*}
neamtic order tensor Q,
\begin{align*}
\frac{\partial Q_{ij}}{\partial t} = - u_{l}\frac{\partial}{\partial x_{l}} Q_{ij} +0.5B_{0}\rho E_{ij} + 2/3B_{0} E_{il}Q_{lj}\ + 2Pe\left( \frac{\partial}{4\partial x_{k}}\left( m_{k}\delta_{ij} + m_{i}\delta_{kj} + m_{j}\delta_{ki} \right) \right) -1/3B_{0} E_{kl}Q_{lk}\delta_{ij}- 4 Q_{ij}\
-Pe\frac{\partial}{\partial x_{k}}m_{k}\delta_{ij}+D_{t}\nabla^{2}Q_{ij} + W_{ij}Q_{jl}-Q_{ij}W_{jl}
\end{align*}
Stokes
\begin{eqnarray*}
\nabla^{2}\mathbf{u} - \boldsymbol{\nabla}\mathrm{P} = -\alpha_{0}\boldsymbol{\nabla}\cdot\boldsymbol{\Sigma}\
\boldsymbol{\nabla}\cdot\mathbf{u}=\mathbf{0}
\end{eqnarray*}
On the surface or boundary of the disk all fluxes are zero, and the velocity is zero. and the solver im using for all the equations are this:
for , rho, m and Q
problemr = fem.petsc.LinearProblem(ar, Lr,
petsc_options={“ksp_type”: “gmres”,
“pc_type”: “hypre”})
uh = problemr.solve()
uh.x.scatter_forward()
and for velocity of the flow:
solver = fem.petsc.LinearProblem(
a, L, bcs, petsc_options={“ksp_type”: “preonly”, “pc_type”: “lu”,
“pc_factor_mat_solver_type”: “mumps”})
w_h = solver.solve()
bcs this is the boundary dirircthlet conditions.
and this is my meshing:
if rank == 0:
gmsh.initialize()
gmsh.model.add(“circle”)
circle = gmsh.model.occ.addDisk(0, 0, 0, radius, radius)
gmsh.model.occ.synchronize()
gmsh.model.addPhysicalGroup(2, [circle], tag=1)
gmsh.model.setPhysicalName(2, 1, “domain”)
boundary = gmsh.model.getBoundary([(2, circle)], oriented=False, recursive=False)
curve_tags = [b[1] for b in boundary if b[0] == 1]
gmsh.model.addPhysicalGroup(1, curve_tags, tag=2)
gmsh.model.setPhysicalName(1, 2, “boundary”)
gmsh.option.setNumber(“Mesh.CharacteristicLengthMax”, h_min)
gmsh.model.mesh.generate(2)
domain, cell_tags, facet_tags = gmshio.model_to_mesh(gmsh.model, comm, 0, gdim=2)
if rank == 0:
gmsh.finalize()
About the degrees of freedom i dont know if this is usefull to you:
Info : Meshing 1D…
Info : Meshing curve 1 (Ellipse)
Info : Done meshing 1D (Wall 0.00163009s, CPU 0.00138s)
Info : Meshing 2D…
Info : Meshing surface 1 (Plane, Frontal-Delaunay)
Info : Done meshing 2D (Wall 3.80429s, CPU 3.7558s)
Info : 45402 nodes 90803 elements
Please format all maths and code so that it is sensbile.
Mathematics can be formatted with standard $ syntax:
$$
a_2
$$
returns
```python
import dolfinx
if hasattr(dolfinx, "__version__"):
print(true)
```
gives you
import dolfinx
if hasattr(dolfinx, "__version__"):
print(true)
In general if your mesh has only 90 000 cells, your problem likely has less than 500 000 dofs.
You can check this by printing
print(Vh.dofmap.index_map.size_global * Vh.dofmap.index_map_bs) if Vh is the spce that uh lives in.
If your problem is this small, parallelization is not likely to speed up the code.
Ok, i share this image of my system of equations. I will check my dofs. But in case that the dof is lower, there is any strategy to make it more faster or accelarete it? can i send my fenicsx script y private? Thanks
I mainly give guidance on public scripts. I do not have time to be a private consultant for users to help them do their research. Please share the scripts on the forum. If you can’t share the full script, make a simplified version that shows how you would set up the structures in your problem on a unit square.
