Hello,
I am trying to solve
\nabla^2 \nabla^2 u = f in the two-dimensional rectangle \Omega = [0, L ]\times [0,h] with boundary conditions
u = u_0 and n^i \partial_i u = v_0 on the boundary \partial \Omega.
I consider an example where I know the solution: u = 1 + \cos(x) + \sin(y). In this case, f = \cos(x) + \sin(y), and on \partial \Omega the BCs read u_0=1 + \cos(x) + \sin(y) and v_0 = (- \sin(x) , \cos( y)). I try to solve this problem with Fenics: I created a minimal working example for you, here is the code:
'''
This code solves the biharmonic equation Nabla Nabla u = f expressed in terms of the function u
run with
clear; clear; python3 mwe.py
example:
python3 mwe.py
'''
from fenics import *
from mshr import *
import ufl as ufl
from dolfin import *
L = 2.2
h = 0.41
alpha = 1e3
i, j, k, l = ufl.indices( 4 )
xdmffile_u = XDMFFile( "solution/u.xdmf" )
xdmffile_check = XDMFFile( "solution/check.xdmf" )
xdmffile_check.parameters.update( {"functions_share_mesh": True, "rewrite_function_mesh": False} )
# create mesh
mesh = RectangleMesh(Point(0, 0), Point(L, h), 20, 10)
mf = MeshFunction("size_t", mesh, mesh.topology().dim() - 1, 0)
eps = 100 * DOLFIN_EPS
r_mesh = mesh.hmin()
class left(SubDomain):
def inside(self, x, on_boundary):
return near(x[0], 0, eps)
left().mark(mf, 2)
class right(SubDomain):
def inside(self, x, on_boundary):
return near(x[0], L, eps)
right().mark(mf, 3)
class top(SubDomain):
def inside(self, x, on_boundary):
return near(x[1], h, eps)
top().mark(mf, 4)
class bottom(SubDomain):
def inside(self, x, on_boundary):
return near(x[1], 0, eps)
bottom().mark(mf, 5)
boundary = 'on_boundary'
# test for surface elements
ds_l = Measure("ds", domain=mesh, subdomain_data=mf, subdomain_id=2)
ds_r = Measure("ds", domain=mesh, subdomain_data=mf, subdomain_id=3)
ds_t = Measure("ds", domain=mesh, subdomain_data=mf, subdomain_id=4)
ds_b = Measure("ds", domain=mesh, subdomain_data=mf, subdomain_id=5)
n = FacetNormal( mesh )
function_space_degree = 4
Q = FunctionSpace( mesh, 'P', function_space_degree )
V = VectorFunctionSpace( mesh, 'P', function_space_degree )
class u_exact_expression( UserExpression ):
def eval(self, values, x):
values[0] = 1.0 + cos(x[0]) + sin(x[1])
def value_shape(self):
return (1,)
class grad_u_expression( UserExpression ):
def eval(self, values, x):
values[0] = -sin( x[0] )
values[1] = cos( x[1] )
def value_shape(self):
return (2,)
class laplacian2_u_expression( UserExpression ):
def eval(self, values, x):
values[0] = cos( x[0] ) + sin( x[1] )
def value_shape(self):
return (1,)
u = Function( Q )
nu = TestFunction( Q )
f = Function( Q )
grad_u = Function( V )
J_u = TrialFunction( Q )
u_exact = Function( Q )
u_exact.interpolate( u_exact_expression( element=Q.ufl_element() ) )
grad_u.interpolate( grad_u_expression( element=V.ufl_element() ) )
f.interpolate( laplacian2_u_expression( element=Q.ufl_element() ) )
u_profile = Expression( '1.0 + cos(x[0]) + sin(x[1])', L=L, h=h, element=Q.ufl_element() )
bc_u = DirichletBC( Q, u_profile, boundary )
F_u = ((u.dx( i ).dx( i ).dx( j )) * (nu.dx( j )) + f * nu) * dx \
- n[j] * (u.dx( i ).dx( i ).dx( j )) * nu * ds
# nitsche's term to implement the second BC (no, I have not included the symmetrizing term because my real problem will be nonlinear)
F_N = alpha / r_mesh * (n[j] * (u.dx( j )) - n[j] * grad_u[j]) * n[k] * (nu.dx( k )) * ds
F = F_u + F_N
bcs = [bc_u]
J = derivative( F, u, J_u )
problem = NonlinearVariationalProblem( F, u, bcs, J )
solver = NonlinearVariationalSolver( problem )
solver.solve()
xdmffile_u.write( u, 0 )
xdmffile_check.write( project( u.dx( i ).dx( i ).dx( j ).dx( j ), Q ), 0 )
xdmffile_check.write( f, 0 )
xdmffile_check.write( project( u.dx( i ).dx( i ).dx( j ).dx( j ) - f, Q ), 0 )
xdmffile_check.close()
I runs fine:
$ python3 mwe.py
Solving nonlinear variational problem.
Newton iteration 0: r (abs) = 5.676e+08 (tol = 1.000e-10) r (rel) = 1.000e+00 (tol = 1.000e-09)
Newton iteration 1: r (abs) = 2.133e-01 (tol = 1.000e-10) r (rel) = 3.757e-10 (tol = 1.000e-09)
Newton solver finished in 1 iterations and 1 linear solver iterations.
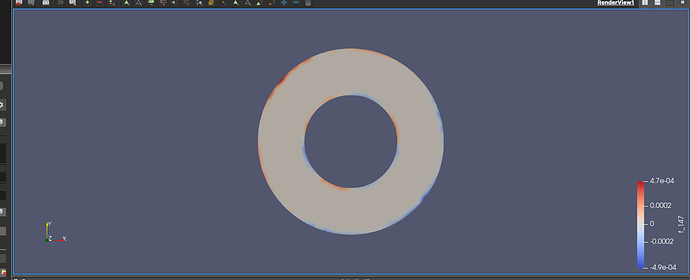
however, when I visualize the solution in Paraview, it takes oddly large values within the rectangle, where it differs from the exact solution:
(The solution satisfied the Dirichlet BCs but then it takes gigantic values within \Omega).
Do you know what I am doing wrong here ?
Thank you ! ![]()