I don’t really understand what your intent is with the terms dx(x) and ds(mesh). dx(x) doesn’t make sense, and perhaps you needed the latter to actually give you a non-zero form (since UFL will optimise out zeros unless wrapped in a constant)?
I’m running dolfinx@main so there are some minor changes to my import statements, but the code is largely the same. Note I use Constants for f and g and I changed the ds and dx terms.
import dolfinx
import numpy as np
import ufl
from dolfinx.fem import (apply_lifting, Constant, dirichletbc, Expression,
form, Function, FunctionSpace, locate_dofs_topological, set_bc,
VectorFunctionSpace
)
from dolfinx.fem.petsc import LinearProblem, assemble_matrix, assemble_vector
from dolfinx.io import XDMFFile
from dolfinx.mesh import locate_entities_boundary, create_rectangle, CellType, GhostMode
from mpi4py import MPI
from petsc4py import PETSc
from petsc4py.PETSc import ScalarType
from ufl import ds, dx, grad, inner, dot
mesh = create_rectangle(MPI.COMM_WORLD, [np.array([0.0, 0.0]),
np.array([10, 10])], [10, 10],
CellType.triangle, GhostMode.shared_facet)
tdim = mesh.topology.dim
fdim = tdim - 1
V = VectorFunctionSpace(mesh, ("Lagrange", 1))
# Define boundary condition on x = 0 or x = 1
u0 = Function(V)
with u0.vector.localForm() as u0_loc:
u0_loc.set(1)
u1 = Function(V)
with u1.vector.localForm() as u1_loc:
u1_loc.set(0)
x0facets = locate_entities_boundary(mesh, fdim,
lambda x: np.isclose(x[0], 0.0))
x1facets = locate_entities_boundary(mesh, fdim,
lambda x: np.isclose(x[0], 10.0))
x0bc = dirichletbc(u0, locate_dofs_topological(V, fdim, x0facets))
x1bc = dirichletbc(u1, locate_dofs_topological(V, fdim, x1facets))
# Define variational problem
u, v = ufl.TrialFunction(V), ufl.TestFunction(V)
x = ufl.SpatialCoordinate(mesh)
f = dolfinx.fem.Constant(mesh, PETSc.ScalarType((0.0, 0.0)))
g = dolfinx.fem.Constant(mesh, PETSc.ScalarType((0.0, 0.0)))
a = form(inner(grad(u), grad(v)) * dx)
L = form(inner(f, v) * dx + inner(g, v) * ds)
A = assemble_matrix(a, bcs=[x0bc, x1bc])
A.assemble()
b = assemble_vector(L)
apply_lifting(b, [a], bcs=[[x0bc, x1bc]])
b.ghostUpdate(addv=PETSc.InsertMode.ADD, mode=PETSc.ScatterMode.REVERSE)
set_bc(b, [x0bc, x1bc])
# Set solver options
opts = PETSc.Options()
opts["ksp_type"] = "cg"
opts["ksp_rtol"] = 1.0e-10
opts["pc_type"] = "gamg"
# Use Chebyshev smoothing for multigrid
opts["mg_levels_ksp_type"] = "chebyshev"
opts["mg_levels_pc_type"] = "jacobi"
# Improve estimate of eigenvalues for Chebyshev smoothing
opts["mg_levels_esteig_ksp_type"] = "cg"
opts["mg_levels_ksp_chebyshev_esteig_steps"] = 20
# Create PETSc Krylov solver and turn convergence monitoring on
solver = PETSc.KSP().create(mesh.comm)
solver.setFromOptions()
# Set matrix operator
solver.setOperators(A)
uh = Function(V)
# Set a monitor, solve linear system, and dispay the solver configuration
# solver.setMonitor(lambda _, its, rnorm: print(f"Iteration: {its}, rel. residual: {rnorm}"))
solver.solve(b, uh.vector)
# solver.view()
uh.x.scatter_forward()
# Save solution in XDMF format
with XDMFFile(MPI.COMM_WORLD, "potential.xdmf", "w") as file:
file.write_mesh(mesh)
file.write_function(uh)
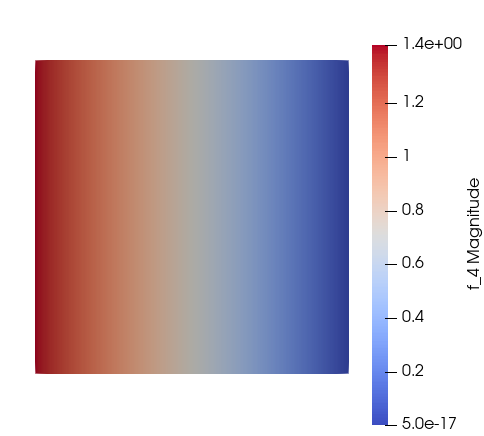
which gives me this: