Resolved by fixing a typo. The code below should work.
I am using FEniCS 2018.1.0
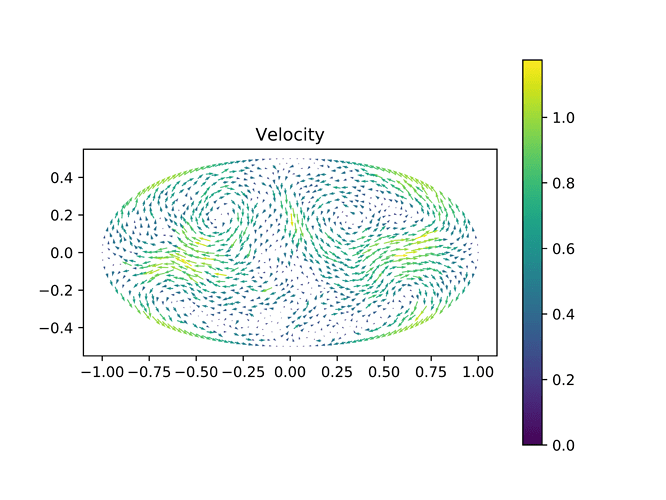
This might be because of the mesh, but the following code blows up for when b is not 1 and the boundary conditions have even harmonics. It is really bizzarre, since it works very well for odd harmonics. I am losing my mind figuring this out!
import matplotlib
matplotlib.use('Agg')
from matplotlib import ticker
import matplotlib.pyplot as plt
from dolfin import *
from mshr import *
def epsilon(u):
return grad(u)+nabla_grad(u)
b=0.3
embryo = Ellipse(Point(0.0, 0.0), 1, b)
mesh = generate_mesh(embryo, 32)
# Define function spaces
P2 = VectorElement('CG', triangle, 5)
P1 = FiniteElement('CG', triangle, 3)
TH = MixedElement([P2, P1])
W = FunctionSpace(mesh, TH)
g = Constant(0.0)
mu = Constant(1.0)
force = Constant((0.0, 0.0))
# Specify Boundary Conditions
boundary = 'on_boundary'
flow_profile = ('-sin(atan2(x[1]/b,x[0]))*sin(nharmonic*atan2(x[1]/b,x[0]))','b*cos(atan2(x[1]/b,x[0]))*sin(nharmonic*atan2(x[1]/b,x[0]))')
bcu = DirichletBC(W.sub(0), Expression(flow_profile, degree=5, b=b, nharmonic=2), boundary)
bc = [bcu]
# Define trial and test functions
(u, p) = TrialFunctions(W)
(v, q) = TestFunctions(W)
a1 = inner( mu*epsilon(u)+p*Identity(2), nabla_grad(v))*dx + div(u)*q*dx
L1 = dot(force,v)*dx + g*q*dx
print('Preliminaries Done')
# Solve system
U = Function(W)
solve(a1==L1, U, bc)
print('Solving Done')
# Get sub-functions
u, p = U.split()
folder='./'
fig=plot(u, title='Velocity')
plt.colorbar(fig)
plt.savefig(folder+'vel.png', dpi=1000)
plt.close()
print('Plotting Done')