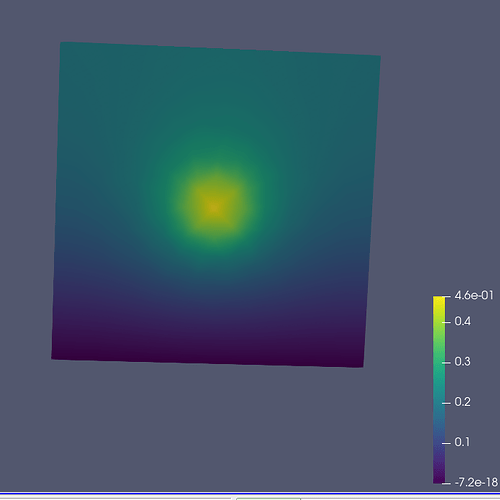
Hi, I am facing a problem with the initial conditions in the heat equation. Basically, when I set the initial condition to be u0(x) = 0 everywhere, the simulation goes wrong and I get weird results, just like if the equation was ignoring the source term and the solution remained 0 everywhere.
import numpy as np
import gmsh
import tqdm
from mpi4py import MPI
from petsc4py import PETSc
from dolfinx import fem, io
from dolfinx.mesh import locate_entities_boundary
from ufl import grad, dx, dot, ds, dS, SpatialCoordinate, TestFunction, TrialFunction, Measure
gdim = 3
mesh_comm = MPI.COMM_WORLD
model_rank = 0
fluid_tag, source_tag = 11, 22
gmsh.initialize()
if mesh_comm.rank == model_rank:
fluid = gmsh.model.occ.addBox(0, 0, 0, 1, 1, 1)
source = gmsh.model.occ.addBox(0.4, 0.4, 0.4, 0.2, 0.2, 0.2)
all_entities = gmsh.model.occ.fragment([(gdim, fluid)], [(gdim, source)])
gmsh.model.occ.synchronize()
all_vols = gmsh.model.occ.getEntities(gdim)
for dim, tag in all_vols:
mass = gmsh.model.occ.getMass(dim, tag)
if np.isclose(mass, 0.2**3):
source = [tag]
else:
fluid = [tag]
gmsh.model.addPhysicalGroup(gdim, source, source_tag)
gmsh.model.setPhysicalName(gdim, source_tag, "source")
gmsh.model.addPhysicalGroup(gdim, fluid, fluid_tag)
gmsh.model.setPhysicalName(gdim, fluid_tag, "fluid")
source_faces = gmsh.model.getBoundary([(gdim, source[0])])
gmsh.model.mesh.field.add("Distance", 1)
gmsh.model.mesh.field.setNumbers(1, "FacesList", [e[1] for e in source_faces])
gmsh.model.mesh.field.add("Threshold", 2)
gmsh.model.mesh.field.setNumber(2, "IField", 1)
gmsh.model.mesh.field.setNumber(2, "LcMin", 0.2 / 3)
gmsh.model.mesh.field.setNumber(2, "LcMax", 3.0 * 0.2)
gmsh.model.mesh.field.setNumber(2, "DistMin", 2 * 0.2)
gmsh.model.mesh.field.setNumber(2, "DistMax", 5 * 0.2)
gmsh.model.mesh.field.add("Min", 5)
gmsh.model.mesh.field.setNumbers(5, "FieldsList", [2])
gmsh.model.mesh.field.setAsBackgroundMesh(5)
gmsh.option.setNumber("Mesh.Algorithm", 7)
gmsh.model.mesh.generate(gdim)
gmsh.model.mesh.optimize("Netgen")
mesh, ct, _ = io.gmshio.model_to_mesh(gmsh.model, mesh_comm, 0, gdim=gdim)
gmsh.finalize()
dx = Measure("dx", domain=mesh)
ds = Measure("ds", domain=mesh)
# Espacios de funciones
V, Q = fem.FunctionSpace(mesh, ("CG", 1)), fem.FunctionSpace(mesh, ("DG", 0))
# Fuente
f = fem.Function(Q)
f.x.array[:] = 0.0
source_cells = ct.find(source_tag)
f.x.array[source_cells] = 50.0
# # Condiciones de contorno
#Condiciones de Dirichlet
def boundary_D(x):
return np.isclose(x[2], 1)
def u_boundary(x):
return 0.0 * x[0]
dofs_D = fem.locate_dofs_geometrical(V, boundary_D)
u_bc = fem.Function(V)
u_bc.interpolate(u_boundary)
bc = fem.dirichletbc(u_bc, dofs_D)
# Condiciones de Neumann
x = SpatialCoordinate(mesh)
g = 0.0 * x[0]
# Parámetros temporales
t = 0 # Start time
T = 10 # Final time
num_steps = 75
dt = T / num_steps # time step size
dt = fem.Constant(mesh, PETSc.ScalarType(dt))
# Condición inicial
def initial_condition(x):
return 0.0 * x[0]
u_n = fem.Function(V)
u_n.interpolate(initial_condition)
uh = fem.Function(V)
uh.interpolate(initial_condition)
# Forma variacional y ensamblar matriz/vector
u, v = TrialFunction(V), TestFunction(V)
a = u * v * dx + dt * dot(grad(u), grad(v)) * dx
L = (u_n + dt * f) * v * dx + dt * g * v * ds
bilinear_form = fem.form(a)
linear_form = fem.form(L)
A = fem.petsc.assemble_matrix(bilinear_form, bcs=[bc])
A.assemble()
b = fem.petsc.create_vector(linear_form)
# Solver
solver = PETSc.KSP().create(mesh.comm)
solver.setOperators(A)
solver.setType(PETSc.KSP.Type.PREONLY)
solver.getPC().setType(PETSc.PC.Type.LU)
# Archivo para guardar el output
xdmf = io.XDMFFile(mesh_comm, 'outputs/source.xdmf', 'w')
xdmf.write_mesh(mesh)
xdmf.write_function(uh, t)
timer = tqdm.tqdm(total=num_steps)
for _ in range(num_steps):
t += dt
timer.update(1)
# Updatear la forma lineal
with b.localForm() as loc_b:
loc_b.set(0)
fem.petsc.assemble_vector(b, linear_form)
# Aplicar condición de dirichlet al vector
fem.petsc.apply_lifting(b, [bilinear_form], [[bc]])
b.ghostUpdate(addv=PETSc.InsertMode.ADD_VALUES, mode=PETSc.ScatterMode.REVERSE)
fem.petsc.set_bc(b, [bc])
# Solve
solver.solve(b, uh.vector)
uh.x.scatter_forward()
# Updatear u_n
u_n.x.array[:] = uh.x.array
# Escribir en archivo
xdmf.write_function(uh, t)
xdmf.close()
However, if I substitute the initial condition in the code above for
def u_boundary(x):
return 0.1 * x[0]
(or any other function that is not zero everywhere) the equation works fine, and I get the expected behavior: the source radiates heat and the temperature rises according to the boundary conditions.
I am a quite loss with this problem, and any suggestions would be appreciated.
Thank you very much in advance!