Yes, the script is similar.
import numpy as np
import ufl
import gmsh
import dolfinx
from petsc4py import PETSc
from dolfinx import fem, mesh, io
from dolfinx.fem.petsc import LinearProblem
from ufl import Measure, SpatialCoordinate, TestFunctions, TrialFunctions, div, exp, inner
from basix.ufl import element, mixed_element
from mpi4py import MPI
from dolfinx import default_scalar_type, plot
from dolfinx.fem import (functionspace, dirichletbc)
from dolfinx.io import (VTXWriter, distribute_entity_data, gmshio, XDMFFile)
# Physical parameters
D = 1
Ht = 1.62 # height till top
Hb = 1.9 # height till bottom
L = 6
H = Ht+Hb
c_x = 0
c_y = 0
r = D/2
# Numerical parameters
resolution = 0.1 # Target characteristic length factor #0.05
# EPS = np.finfo(float).eps # Machine epsilon for float
model_rank = 0
mesh_comm = MPI.COMM_WORLD
gdim=2
# Create gmsh geometry
gmsh.initialize()
# Create channel
rectangle = gmsh.model.occ.addRectangle(-L/2, -Hb, 0, L, H)
# Create circle
obstacle = gmsh.model.occ.addDisk(c_x, c_y, 0, r, r)
gmsh.model.occ.cut([(gdim, rectangle)], [(gdim, obstacle)])
gmsh.model.occ.synchronize()
# # Set mesh resolution
gmsh.option.setNumber("Mesh.CharacteristicLengthFactor", resolution)
gmsh.option.setNumber("Mesh.Algorithm", 8)
# gmsh.option.setNumber("Mesh.RecombinationAlgorithm", 2)
# gmsh.option.setNumber("Mesh.RecombineAll", 1)
# gmsh.option.setNumber("Mesh.SubdivisionAlgorithm", 1)
gmsh.model.mesh.generate(gdim)
gmsh.model.mesh.setOrder(2)
gmsh.model.mesh.optimize("Netgen")
# # gmsh.fltk().run()
# Add physical tag for bulk
fluid_marker = 1
if mesh_comm.rank == model_rank:
volumes = gmsh.model.getEntities(dim=gdim)
assert (len(volumes) == 1)
gmsh.model.addPhysicalGroup(volumes[0][0], [volumes[0][1]], fluid_marker)
gmsh.model.setPhysicalName(volumes[0][0], fluid_marker, "Fluid")
# # Add physical tag for boundaries
# boundary = gmsh.model.getBoundary(
# [(2, surface)], combined=False, oriented=False, recursive=False)
# for i, (boundary) in enumerate(boundary):
# gmsh.model.addPhysicalGroup(boundary[0], [boundary[1]], i)
gmsh.write("mesh2.msh")
# # Convert gmsh mesh to dolfinx mesh
mesh_obj, _, _ = gmshio.model_to_mesh(gmsh.model, mesh_comm, model_rank, gdim=gdim)
gmsh.finalize()
# Create finite element spaces
# Function spaces for the velocity and for the pressure
k = 1
Q_el = element("BDM", mesh_obj.basix_cell(), k)
P_el = element("DG", mesh_obj.basix_cell(), k - 1)
V_el = mixed_element([Q_el, P_el])
V = functionspace(mesh_obj, V_el)
# Get subspace of V
V0 = V.sub(0)
Q, _ = V0.collapse()
# Define test, trial and solution functshoes that fits feet designion
# u = TrialFunctions(V)
# v = TestFunctions(V)
#
# p = TrialFunctions(V)
# q = TestFunctions(V)
(u, p) = ufl.TrialFunctions(V)
(v, q) = ufl.TestFunctions(V)
# Define boundary conditions
def boundary_noflow(x):
return np.logical_or(np.isclose(x[1], -Hb), np.isclose(x[1], Ht), np.isclose(x[0]**2 + x[1]**2, r**2))
def boundary_inflow(x):
return np.isclose(x[0], -L/2)
fdim = mesh_obj.topology.dim - 1
facets_noflow = mesh.locate_entities_boundary(mesh_obj, fdim, boundary_noflow)
dofs_noflow = fem.locate_dofs_topological((V0, Q), fdim, facets_noflow)
# Walls
# u_noflow = np.array((0,) * mesh_obj.geometry.dim, dtype=PETSc.ScalarType)
# bc_noflow = dirichletbc(u_noflow, dofs_noflow, V0)
# Define a function for the inflow velocity on the full vector space V
u_noflow_func = fem.Function(Q)
# Define a function to set the inflow profile
def noflow_profile(x):
values = np.zeros((mesh_obj.geometry.dim, x.shape[1]))
values[0, :] = 0.0 # Set x-component of the velocity
return values
# Interpolate the inflow profile into the function
u_noflow_func.interpolate(noflow_profile)
# Apply the Dirichlet BC using the function
bc_noflow = fem.dirichletbc(u_noflow_func, dofs_noflow, V0)
# # InFlow
facets_inflow = mesh.locate_entities_boundary(mesh_obj, fdim, boundary_inflow)
dofs_inflow = fem.locate_dofs_topological((V0, Q), fdim, facets_inflow)
# u_inflow = np.array((1,) * mesh_obj.geometry.dim, dtype=PETSc.ScalarType)
# bc_inflow = fem.dirichletbc(u_inflow, dofs_inflow, V0)
# Define a function for the inflow velocity on the full vector space V
u_inflow_func = fem.Function(Q)
# Define a function to set the inflow profile
def inflow_profile(x):
values = np.zeros((mesh_obj.geometry.dim, x.shape[1]))
values[0, :] = 1.0 # Set x-component of the velocity
return values
# Interpolate the inflow profile into the function
u_inflow_func.interpolate(inflow_profile)
# Apply the Dirichlet BC using the function
bc_inflow = fem.dirichletbc(u_inflow_func, dofs_inflow, V0)
bcs = [bc_noflow, bc_inflow]
#
#
#
#Defining the variational problem
f = - fem.Constant(mesh_obj, PETSc.ScalarType(0))
# Define the bilinear form correctly
a = (ufl.inner(u, v) + ufl.div(v)*p + ufl.div(u)*q) * ufl.dx
L = -f*q*ufl.dx
#solving the equation
problem = LinearProblem(
a,
L,
bcs=bcs,
petsc_options={"ksp_type": "preonly", "pc_type": "lu", "pc_factor_mat_solver_type": "mumps"},
)
try:
w_h = problem.solve()
except PETSc.Error as e: # type: ignore
if e.ierr == 92:
print("The required PETSc solver/preconditioner is not available. Exiting.")
print(e)
exit(0)
else:
raise e
sigma_h, u_h = w_h.split()
with io.XDMFFile(mesh_obj.comm, "out_mixed_poisson/u.xdmf", "w") as file:
file.write_mesh(mesh_obj)
file.write_function(u_h)
# Different way 2
gdim = mesh_obj.geometry.dim
V1 = fem.functionspace(mesh_obj, ("Lagrange", 2, (gdim,)))
u1 = fem.Function(V1, dtype=default_scalar_type)
u1.interpolate(sigma_h)
with dolfinx.io.VTXWriter(mesh_obj.comm, "album1.bp", u1, engine="BP4") as vtx:
vtx.write(0.0)
And this is the distribution profile for velocity reported by Fig 1. Hele-Shaw flow past a circle · An album of computational fluid motion
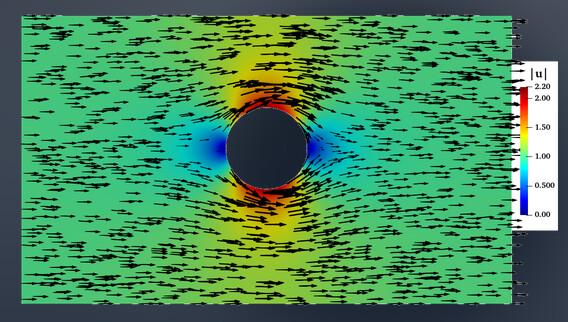
As you can see, my velocity profile reported previously is different.
I don’t understand the reason of this discrepancy.



