Im a rookie in Fenicsx, Im confused about how to define the function phi_0 in picture 3 so that I can put phi_0 into a ( u , v ) and do some advanced work.
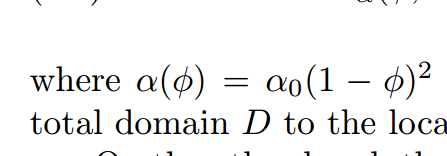
my code is as followed:
# create a mesh
msh = create_rectangle(
MPI.COMM_WORLD, [np.array([0, 0]), np.array([1, 1])], [32, 32], CellType.triangle
)
#function to mark x=0
def in_boundary(x):
return np.isclose(x[0],0.0)
#function to mark y=0,y=1
def wall_boundary(x):
return np.logical_or(
np.logical_or(np.isclose(x[1], 0.0), np.isclose(x[1], 1.0))
)
#function to mark x=1
def in_boundary(x):
return np.isclose(x[0],1.0)
# in_velocity
def in_velocity_expression(x):
return np.stack((np.ones(x.shape[1]), np.zeros(x.shape[1])))
#define V and Q
P2 = element("Lagrange", msh.basix_cell(), 2, shape=(msh.geometry.dim,))
P1 = element("Lagrange", msh.basix_cell(), 1)
V, Q = functionspace(msh, P2), functionspace(msh, P1)
# No-slip condition on boundaries where y=0,y=1
noslip = np.zeros(msh.geometry.dim, dtype=PETSc.ScalarType)
facets = locate_entities_boundary(msh, 1, wall_boundary)
bc0 = dirichletbc(noslip, locate_dofs_topological(V, 1, facets), V)
# Driving velocity condition on boundary where x=0
in_velocity = Function(V)
in_velocity.interpolate(in_velocity_expression)
facets = locate_entities_boundary(msh, 1, in_boundary)
bc1 = dirichletbc(in_velocity, locate_dofs_topological(V, 1, facets))
# Collect Dirichlet boundary conditions
bcs = [bc0, bc1]
# alpha_0
alpha_0=Constant(mesh, PETSc.ScalarType(1))
# phi_0
# Define variational problem
(u, p) = ufl.TrialFunction(V), ufl.TrialFunction(Q)
(v, q) = ufl.TestFunction(V), ufl.TestFunction(Q)
f = Constant(msh, (PETSc.ScalarType(0), PETSc.ScalarType(0)))
a = form([[inner(grad(u), grad(v)) * dx + inner(alpha_0*(1-phi_0)*(1-phi_0)*u,v)*dx, -inner(p, div(v)) * dx], [inner(div(u), q) * dx, None]])
L = form([inner(f, v) * dx, inner(Constant(msh, PETSc.ScalarType(0)), q) * dx])
I would appreciate your help!





